Problema cn trasformata di Laplace
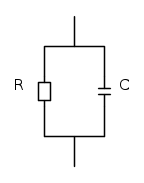
Salve,vorrei se possibile qualche aiuto su un dubbio relativo alla trasformata di Laplace.In particolare se ho un semplice bipolo RC come in figura
e voglio trovare il segnale di ingresso che rende infinita tale impedenza allora ho che l'ammettenza del bipolo nel dominio trasformato è

se il segnale di ingresso è un esponenziale
allora
quindi se
allora
quindi antitrasformando
quello che non capisco (ammesso che il procedimensto sia corretto..ma penso di si) è come mai la corrente trasformata viene CV quindi dimensionalmente una carica e non una corrente.Qualcuno sa darmi una mano? Grazie
e voglio trovare il segnale di ingresso che rende infinita tale impedenza allora ho che l'ammettenza del bipolo nel dominio trasformato è

se il segnale di ingresso è un esponenziale

allora

quindi se

allora

quindi antitrasformando

quello che non capisco (ammesso che il procedimensto sia corretto..ma penso di si) è come mai la corrente trasformata viene CV quindi dimensionalmente una carica e non una corrente.Qualcuno sa darmi una mano? Grazie
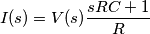
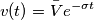 la corrente diventa
la corrente diventa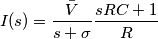
 che carica istantaneamente la capacità: se calcoli l'integrale di corrente ottieni infatti
che carica istantaneamente la capacità: se calcoli l'integrale di corrente ottieni infatti
 , quindi non vedrai entrare altra corrente nel circuito.
, quindi non vedrai entrare altra corrente nel circuito.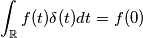 che ha ovviamente le dimensioni di
che ha ovviamente le dimensioni di  , quindi
, quindi  è dimensionalmente l'inverso di un tempo, ossia ha come dimensione l'Hz, però non saprei dimostrartelo a partire dalla definizione, forse considerandolo come
è dimensionalmente l'inverso di un tempo, ossia ha come dimensione l'Hz, però non saprei dimostrartelo a partire dalla definizione, forse considerandolo come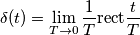
 ha una dimensione
ha una dimensione ![[As] [As]](/forum/latexrender/pictures/bd5d59a47111589b12e7c2d29cbe4ac8.png) in quanto una corrente è stata integrata nel tempo dall'operatore della trasformata. Per questo motivo penso che portando
in quanto una corrente è stata integrata nel tempo dall'operatore della trasformata. Per questo motivo penso che portando  al secondo membro le dimensioni dovrebbero tornare.
al secondo membro le dimensioni dovrebbero tornare. 