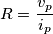problema con Thevenin
Salve,
paleso pubblicamente la mia clamorosa ignoranza
Alcuni testi (e anche un mio professore) dicono che:
Ossia preso un bipolo l'impedenza equivalente vista ai due morsetti la si può valutare come rapporto tra tensione di circuito aperto e corrente di corto circuito.
Wikipedia, qualche libro, il professore dicono che questa relazione è vera: a me personalmente non piace affatto.
1) Se il bipolo è un generatore di tensione ideale. Ci potrebbe stare che la corrente di corto circuito di un generatore ideale è infinita e quindi la resistenza viene nulla. Ma a me chiudere in corto un generatore ideale da' qualche problema: il generatore impone tra i due morsetti una differenza di potenziale fissa e il corto circuito una differenza di potenziale nulla. Mi pare un controsenso teorico.
2) Generatore di corrente ideale. La tensione a vuoto sarebbe infinita.
3) qualsiasi rete puramente passiva. Se la rete non contiene generatori la tensione misurata ai morsetti è sicuramente nulla. Anche la corrente è sicuramente nulla. Il rapporto 0/0 è indeterminato. Quindi applicando questa definizione l'impedenza "equivalente" di un solo resistore non si può calcolare.
A me pare un metodo che non porta risultati, credo sia più corretto stimolare il circuito con un generatore esterno noto e vedere quanta corrente scorre su di lui per vedere l'impedenza equivalente di un bipolo.
Questi sono i miei ragionamenti. I testi e chi insegna dice che quella formula è vera. Sono sicuro di sbagliare io, ma non so dove sbaglio. Potete guidarmi a capire?
Daivde
paleso pubblicamente la mia clamorosa ignoranza
Alcuni testi (e anche un mio professore) dicono che:
la resistenza equivalente può essere ottenuta:
Ossia preso un bipolo l'impedenza equivalente vista ai due morsetti la si può valutare come rapporto tra tensione di circuito aperto e corrente di corto circuito.
Wikipedia, qualche libro, il professore dicono che questa relazione è vera: a me personalmente non piace affatto.
1) Se il bipolo è un generatore di tensione ideale. Ci potrebbe stare che la corrente di corto circuito di un generatore ideale è infinita e quindi la resistenza viene nulla. Ma a me chiudere in corto un generatore ideale da' qualche problema: il generatore impone tra i due morsetti una differenza di potenziale fissa e il corto circuito una differenza di potenziale nulla. Mi pare un controsenso teorico.
2) Generatore di corrente ideale. La tensione a vuoto sarebbe infinita.
3) qualsiasi rete puramente passiva. Se la rete non contiene generatori la tensione misurata ai morsetti è sicuramente nulla. Anche la corrente è sicuramente nulla. Il rapporto 0/0 è indeterminato. Quindi applicando questa definizione l'impedenza "equivalente" di un solo resistore non si può calcolare.
A me pare un metodo che non porta risultati, credo sia più corretto stimolare il circuito con un generatore esterno noto e vedere quanta corrente scorre su di lui per vedere l'impedenza equivalente di un bipolo.
Questi sono i miei ragionamenti. I testi e chi insegna dice che quella formula è vera. Sono sicuro di sbagliare io, ma non so dove sbaglio. Potete guidarmi a capire?
Daivde
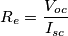


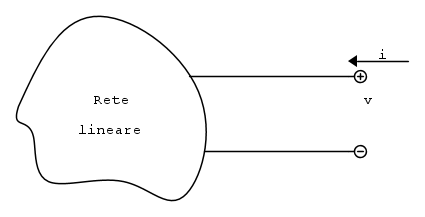

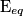 e R.
e R.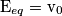 con i=0
con i=0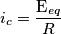 con v=0
con v=0
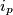 che alimenti i morsetti di ingresso della nostra rete lineare e misurare o calcolare la tensione
che alimenti i morsetti di ingresso della nostra rete lineare e misurare o calcolare la tensione 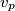 ai loro capi (non e' più' solido: e' un'alternativa).
ai loro capi (non e' più' solido: e' un'alternativa).