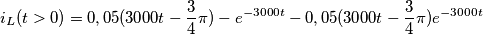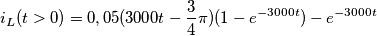Circuito RL nel Dominio del Tempo
Salve, il testo dell'esercizio è il seguente:
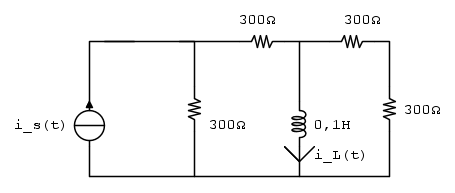
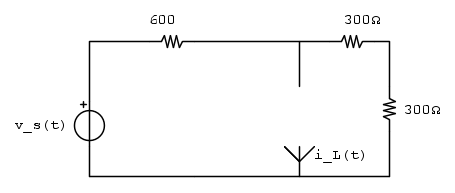
Calcolare per t>0 , operando nel dominio del tempo, sapendo che
per t>0 , operando nel dominio del tempo, sapendo che


Tentativo di risoluzione:

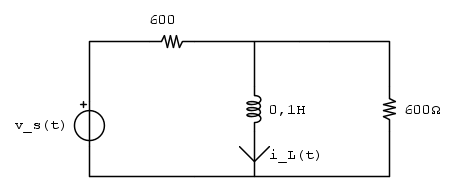
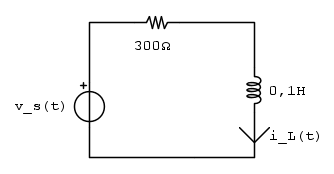
per t>0
Applico la trasformazione di una sorgente

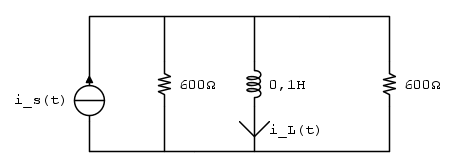
Sommo le due resistenze in serie e l'induttore diventa un circuito aperto(perché se ho capito bene siamo nel regime sinusoidale)

Vorrei capire se ci sono errori(presumo di si), grazie per chi mi aiuta
Calcolare
 per t>0 , operando nel dominio del tempo, sapendo che
per t>0 , operando nel dominio del tempo, sapendo che

Tentativo di risoluzione:

per t>0
Applico la trasformazione di una sorgente

Sommo le due resistenze in serie e l'induttore diventa un circuito aperto(perché se ho capito bene siamo nel regime sinusoidale)

Vorrei capire se ci sono errori(presumo di si), grazie per chi mi aiuta

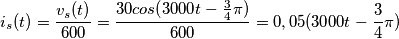
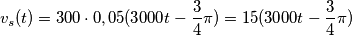
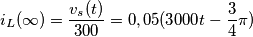
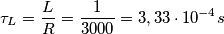
![i_L(t>0) = i_L(\infty) + [i_L(0) - i_L(\infty)]e^{-\frac{t}{\tau_{L} } } i_L(t>0) = i_L(\infty) + [i_L(0) - i_L(\infty)]e^{-\frac{t}{\tau_{L} } }](/forum/latexrender/pictures/2252e97acd66947afaf909e1f7d13aa0.png)
![i_L(t>0) = 0,05(3000t-\frac{3}{4} \pi) + [-1 - 0,05(3000t-\frac{3}{4} \pi)] e^{-3000t} i_L(t>0) = 0,05(3000t-\frac{3}{4} \pi) + [-1 - 0,05(3000t-\frac{3}{4} \pi)] e^{-3000t}](/forum/latexrender/pictures/54f5358769516039ff55beeb3a4ac876.png)