La Zo di una linea di trasmissione.
Buon giorno.
L'impedenza Zo di una linea di trasmissione, vista dai morsetti di alimentazione della stessa, ha, come noto, un valore costante (indipendentemente dalla lunghezza della linea stessa).
Sappiamo che Zo tiene conto della R , L, G e C per unità (m, km) e che costituiscono celle infinitesimali della linea stessa. E che di queste celle infinitesimali ce ne sono, ovviamente, un numero infinito.
Ma,chiedo,come si può impostare un'espressione matematica che tenga conto di tutto ciò e che dimostri che Zo è sempre la stessa in ogni punto?
Vi ringrazio e saluto tutti.
L'impedenza Zo di una linea di trasmissione, vista dai morsetti di alimentazione della stessa, ha, come noto, un valore costante (indipendentemente dalla lunghezza della linea stessa).
Sappiamo che Zo tiene conto della R , L, G e C per unità (m, km) e che costituiscono celle infinitesimali della linea stessa. E che di queste celle infinitesimali ce ne sono, ovviamente, un numero infinito.
Ma,chiedo,come si può impostare un'espressione matematica che tenga conto di tutto ciò e che dimostri che Zo è sempre la stessa in ogni punto?
Vi ringrazio e saluto tutti.
 , partendo da
, partendo da  :
: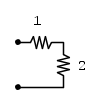
 .
. è legato al precedente così:
è legato al precedente così:
 -esimo corrisponde a questo:
-esimo corrisponde a questo: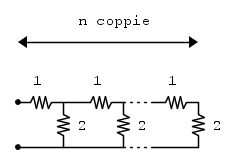
 -esimo è questo:
-esimo è questo: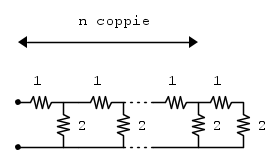

 , che è proprio la risposta alla tua domanda.
, che è proprio la risposta alla tua domanda. , allora:
, allora:



 , abbiamo generato una successione decrescente e inferiormente limitata, per le quali il limite esiste per forza.
, abbiamo generato una successione decrescente e inferiormente limitata, per le quali il limite esiste per forza.