Densità di portatori di carica in un metallo
Buongiorno a tutti,
mi è venuto un dubbio sul calcolo del numero (o meglio densità) di portatori liberi di carica (elettroni) in un metallo. Purtroppo non sono riuscito a trovare ulteriori approfondimenti sul materiale a mia disposizione, chiunque possa/voglia darmi una mano, anche solo con link a pdf/documenti etc... mi darà un grosso aiuto
Supponendo la banda di conduzioni parabolica (pongo lo zero dell'energia al fondo della banda):

(ove è la massa efficace)
è la massa efficace)
si ricava la solita densità di stati:

Per calcolare il numero di portatori si effetua l'integrale:

con la solita distribuzione di Fermi-Dirac, e
la solita distribuzione di Fermi-Dirac, e  la costante di Boltzmann.
la costante di Boltzmann.
La mia domanda riguarda l'estremo inferiore dell'integrale precedente: se ho capito bene, gli elettroni in banda di conduzione lontani dal livello di Fermi per più di
per più di  non partecipano alla conduzione, è corretto?
non partecipano alla conduzione, è corretto?
Questo fatto può essere giustificato poiché gli elettroni (pur in banda di conduzione) troppo lontani dalla non riescono, in pratica, a muoversi (=partecipare alla conduzione) sotto l'effetto di un campo elettrico?
non riescono, in pratica, a muoversi (=partecipare alla conduzione) sotto l'effetto di un campo elettrico?
Ringraziando nuovamente per la pazienza e la collaborazione, auguro una buona Domenica a tutto il forum!
mi è venuto un dubbio sul calcolo del numero (o meglio densità) di portatori liberi di carica (elettroni) in un metallo. Purtroppo non sono riuscito a trovare ulteriori approfondimenti sul materiale a mia disposizione, chiunque possa/voglia darmi una mano, anche solo con link a pdf/documenti etc... mi darà un grosso aiuto
Supponendo la banda di conduzioni parabolica (pongo lo zero dell'energia al fondo della banda):

(ove
 è la massa efficace)
è la massa efficace)si ricava la solita densità di stati:

Per calcolare il numero di portatori si effetua l'integrale:

con
 la solita distribuzione di Fermi-Dirac, e
la solita distribuzione di Fermi-Dirac, e  la costante di Boltzmann.
la costante di Boltzmann.La mia domanda riguarda l'estremo inferiore dell'integrale precedente: se ho capito bene, gli elettroni in banda di conduzione lontani dal livello di Fermi
 per più di
per più di  non partecipano alla conduzione, è corretto?
non partecipano alla conduzione, è corretto?Questo fatto può essere giustificato poiché gli elettroni (pur in banda di conduzione) troppo lontani dalla
 non riescono, in pratica, a muoversi (=partecipare alla conduzione) sotto l'effetto di un campo elettrico?
non riescono, in pratica, a muoversi (=partecipare alla conduzione) sotto l'effetto di un campo elettrico? Ringraziando nuovamente per la pazienza e la collaborazione, auguro una buona Domenica a tutto il forum!
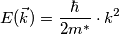
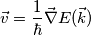
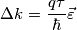
![[-k,k] [-k,k]](/forum/latexrender/pictures/67d55b286f63b3a3eba5c76a9f2c936a.png) ora hai che il tuo range di numeri d'onda è pari a
ora hai che il tuo range di numeri d'onda è pari a 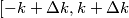 di conseguenza molti elettroni avranno il loro elettrone con numero d'onda opposto e di conseguenza non potranno generare una corrente (e questi sono proprio quelli molto al di sotto del livello di Fermi), molti altri però avendo subito la variazione del loro numero d'onda dovuta al campo non sono più bilanciati da un altro elettrone e possono attuare una corrente.
di conseguenza molti elettroni avranno il loro elettrone con numero d'onda opposto e di conseguenza non potranno generare una corrente (e questi sono proprio quelli molto al di sotto del livello di Fermi), molti altri però avendo subito la variazione del loro numero d'onda dovuta al campo non sono più bilanciati da un altro elettrone e possono attuare una corrente.

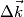 fa si che gli elettroni vicino al livello di Fermi riescano a salire in banda di conduzione. Ciò che succede è che:
fa si che gli elettroni vicino al livello di Fermi riescano a salire in banda di conduzione. Ciò che succede è che: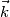 degli elettroni in banda di conduzione (e delle lacune in banda di valenza), generando una corrente.
degli elettroni in banda di conduzione (e delle lacune in banda di valenza), generando una corrente.