esercizio con potenziale elettrico
Questo esercizio che immagino per voi sia semplicissimo, non riesco a risolverlo.
Il potenziale elettrico in un punto qualunque del piano xy è:

V è espresso in volt ed X e Y in metri, si determinino la posizione e la carica di ciascuna delle particelle che creano questo potenziale
per trovare le coordinate della carica prendo un punto qualsiasi che la rappresenta ma dopo che faccio?
ma dopo che faccio?
Potrei ricavarmi le coordinate del campo elettrico derivando il potenziale V ? E poi trovare la distanza tra i due punti (x,y) e (a,b) e metterli in relazione mediante
Ma sto dicendo stupidaggini, chi mi aiuta?
Il potenziale elettrico in un punto qualunque del piano xy è:

V è espresso in volt ed X e Y in metri, si determinino la posizione e la carica di ciascuna delle particelle che creano questo potenziale
per trovare le coordinate della carica prendo un punto qualsiasi che la rappresenta
 ma dopo che faccio?
ma dopo che faccio?Potrei ricavarmi le coordinate del campo elettrico derivando il potenziale V ? E poi trovare la distanza tra i due punti (x,y) e (a,b) e metterli in relazione mediante

Ma sto dicendo stupidaggini, chi mi aiuta?
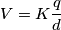
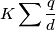
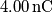 a
a 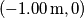
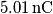 a
a 
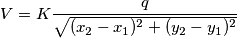
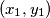 è il punto dove presente la carica puntiforme e
è il punto dove presente la carica puntiforme e  rappresenta il punto dove si misurar il potenziale
rappresenta il punto dove si misurar il potenziale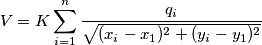
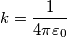
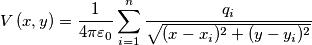
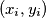 sono le coordinate relative al punto dove e' ubicata la carica qi.
sono le coordinate relative al punto dove e' ubicata la carica qi.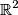 , ma quanto tempo ci vuole per rispondere?
, ma quanto tempo ci vuole per rispondere? in un pomeriggio ma la singolarità gli era comunque sfuggita!
in un pomeriggio ma la singolarità gli era comunque sfuggita!