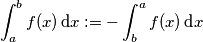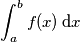ElectroYou

Campo elettrico generato da una distribuzione lineare uniforme di carica.pdf: (237.45 KiB) Scaricato 244 volte

In riferimento all'allegato ed in generale nel calcolo dei campi prodotti da distribuzioni continue, come si fa a stabilire l'ordine degli estremi di integrazione? Uno scambio degli estremi determina un cambio di segno e quindi di verso del campo ma questo non è possibile in quanto il verso del campo dipende dal segno della carica e non dall'ordine degli estremi. Nell'allegato si integra da $-\pi/2$ a $\pi/2$ . perché non si sarebbe potuto integrare tra $\pi/2$ e $-\pi/2$ ? Quello che si fa è sommare contributi infinitesimi quindi o si comincia dal basso o dall'alto a sommare il risultato non dovrebbe cambiare e invece cambia segno.

quapakko ha scritto:... il risultato non dovrebbe cambiare e invece cambia segno.

E infatti non cambia in quanto se integri per angolo crescente il differenziale $\text{d}\theta$ è positivo, se integri per angoli decrescenti, sarà negativo e quindi dovrai scrivere 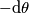$-\text{d}\theta$ .

Quindi $\int_{\pi/2}^{-\pi/2} \sin \theta(-d\theta)=-\int_{\pi/2}^{-\pi/2} \sin \theta d\theta=\int_{-\pi/2}^{\pi/2} \sin\theta d\theta$ .
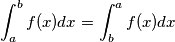Facendo questo ragionamento non risulterebbe sempre $\int_{a}^{b} f(x)dx=\int_{b}^{a} f(x)dx$ ? Basterebbe prendere

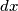negativo al secondo membro per verificare un'uguaglianza che non è vera stando alla proprietà degli integrali sullo scambio degli estremi di integrazione.

No, probabilmente non sono riuscito a spiegarmi; intendevo dire che, dal mio punto di vista, ovvero dal basso della mia incompetenza matematica, quando vedo un integrale che ha l'estremo inferiore maggiore dell'estremo superiore (anche se so che farò drizzare i capelli ai matematici del Forum,

PietroBaima per primo :mrgreen:

), considero il differenziale dx negativo (e viceversa), di conseguenza, nel caso particolare in oggetto, quando andiamo a scrivere la carica infinitesima dq associata ad un tratto dz del filo carico come $\text{d}q=\lambda\, \text{d}z$ , dz dovrà essere maggiore di zero visto che dq dovrà avere il segno di $\lambda$ , ne segue che, integrando da $\pi/2$ a $-\pi/2$ , ed essendo quindi $\text{d} \theta$ negativo, andrei a scrivere

$\text{d}z=R(-\text{d} \theta)$

Vedrai comunque che i veri Matematici del Forum sapranno di certo darti una spiegazione migliore del mio "idraulico" pensiero.

Mah, prendere un $\text{d}\cdot$ negativo non è una idea poi così orripilante.
Riemann protesterebbe, ma Lebesgue no.

Tutto chiaro a parte questo dubbio che ora non riesco a risolvere:

Facendo questo ragionamento non risulterebbe sempre $\int_{a}^{b} f(x)dx=\int_{b}^{a} f(x)dx$ ? Basterebbe prendere dx negativo al secondo membro per verificare un'uguaglianza che non è vera stando alla proprietà degli integrali sullo scambio degli estremi di integrazione.

Se ti è tutto chiaro, non dovresti avere quel dubbio, sostanzialmente (anche se inconsciamente

) ho proprio cercato di dirti come mi spiego quell'uguaglianza

$\int_{a}^{b} f(x)\, \text{d}x:=-\int_{b}^{a} f(x)\, \text{d}x$

che normalmente viene data come definizione, per estendere il significato del simbolo

$\int_{a}^{b} f(x)\, \text{d}x$

anche per a>b.

La risposta alla tua domanda iniziale poteva quindi esserti data semplicemente ricordandotela, senza andare a farti fare confusione.

ElectroYou

Campo elettrostatico distribuzioni continue

Campo elettrostatico distribuzioni continue

Re: Campo elettrostatico distribuzioni continue

Re: Campo elettrostatico distribuzioni continue

Re: Campo elettrostatico distribuzioni continue

Re: Campo elettrostatico distribuzioni continue

Re: Campo elettrostatico distribuzioni continue

Re: Campo elettrostatico distribuzioni continue