Circuito in Regime Variabile
Inviato: 31 dic 2008, 14:32Ciao a tutti
ho il seguente circuito:
la rete è a riposo per t<0 e l'interruttore è aperto. A t=0 l'interruttore viene chiuso. Devo ricavare le due correnti che scorrono nei due induttori.
Ho impostato il sistema con le equazioni differenziali e sono arrivato ad un'equazione differenziale di terzo grado con incognita iL1. Per l'equazione omogenea non ci sono problemi.
Non so però in che forma devo cercare la soluzione particolare, perché questo circuito non ammette soluzione per iL1 in regime stazionario in quanto c'è un generatore di tensione in corto
come posso procedere??
Grazie a tutti
ho il seguente circuito:
- esempio6vi8.png (2.67 KiB) Osservato 8210 volte
la rete è a riposo per t<0 e l'interruttore è aperto. A t=0 l'interruttore viene chiuso. Devo ricavare le due correnti che scorrono nei due induttori.
Ho impostato il sistema con le equazioni differenziali e sono arrivato ad un'equazione differenziale di terzo grado con incognita iL1. Per l'equazione omogenea non ci sono problemi.
Non so però in che forma devo cercare la soluzione particolare, perché questo circuito non ammette soluzione per iL1 in regime stazionario in quanto c'è un generatore di tensione in corto
come posso procedere??Grazie a tutti
.
le cui soluzioni sono 
e 
dove B e D sono costanti da determinare imponendo le condizioni iniziali (ho messo D invece di C per non confonderlo col condensatore).
dove A è possibile determinarla direttamente dall'equaizone differenziali sostituendo a iL1, iL1p, ottenendo quindi 
->
. 
-> t=0 
.![U_{C1}=L1\frac{d}{dt}i_{L1}=L_1\frac{d}{dt}[Bcos(1000t)+Dsin(1000t)+At]=L_1*(1000*D*cos(1000t)+2)](/forum/latexrender/pictures/87733af16542131129b04f9c90ac8143.png "U_{C1}=L1\frac{d}{dt}i_{L1}=L_1\frac{d}{dt}[Bcos(1000t)+Dsin(1000t)+At]=L_1*(1000*D*cos(1000t)+2)")
->t=0->
->D=-2*10^(-3).
![\[
\frac{{d^3 i}}
{{dt^3 }} + a^2 \frac{{di}}
{{dt}} = b
\]](/forum/latexrender/pictures/81cfd1ec7fa245ada2cce0cbeec65142.png "\[
\frac{{d^3 i}}
{{dt^3 }} + a^2 \frac{{di}}
{{dt}} = b
\]")
![\[\left( {ho\,\,scritto\,\,a^2 \,\,per\,\,convenienza\,\,di\,\,calcolo } \right)\]](/forum/latexrender/pictures/bdc62d6b13404c6e7db21dace24cddec.png "\[\left( {ho\,\,scritto\,\,a^2 \,\,per\,\,convenienza\,\,di\,\,calcolo } \right)\]")
![\[
i(t) = - \frac{b}
{{a^3 }}\sin (at) + \frac{b}
{{a^2 }}t
\]](/forum/latexrender/pictures/b2a9322420953712bf05c1a78c7e95bc.png "\[
i(t) = - \frac{b}
{{a^3 }}\sin (at) + \frac{b}
{{a^2 }}t
\]")
![\[\begin{gathered}a^2 = \frac{{L_1 + L_2 }}{{C \cdot L_1 \cdot L_2 }} \hfill \\b = \frac{{V_{s1} }}
{{C \cdot L_1 \cdot L_2 }} \hfill \\ \end{gathered} \]](/forum/latexrender/pictures/7eb9ddbfd362807dc08cc87ecf63bb5f.png "\[\begin{gathered}a^2 = \frac{{L_1 + L_2 }}{{C \cdot L_1 \cdot L_2 }} \hfill \\b = \frac{{V_{s1} }}
{{C \cdot L_1 \cdot L_2 }} \hfill \\ \end{gathered} \]")
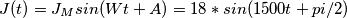
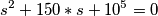mentre la soluzione scrive 
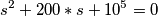e non capisco dove sbaglio