Metodo dei Pot. Nodali in circuito con Generatore Dipendente
Buongiorno a tutti,
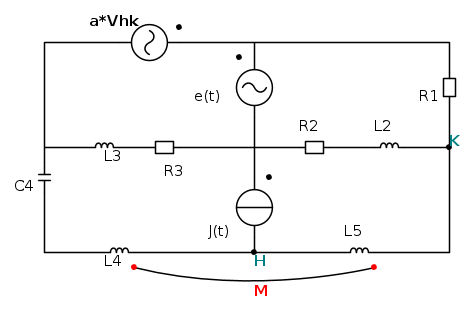
questo è un altro eserciziaccio in cui sono incappato . Si chiede di scrivere e risolvere un sistema completo di equazioni di equilibrio usando il metodo dei Potenziali Nodali , e di ricavare potenza attiva, reattiva e apparente erogate dal generatore di tensione e(t).
. Si chiede di scrivere e risolvere un sistema completo di equazioni di equilibrio usando il metodo dei Potenziali Nodali , e di ricavare potenza attiva, reattiva e apparente erogate dal generatore di tensione e(t).
Ringrazio anticipatamente chiunque mi aiuterà nell' impresa.
questo è un altro eserciziaccio in cui sono incappato
 . Si chiede di scrivere e risolvere un sistema completo di equazioni di equilibrio usando il metodo dei Potenziali Nodali , e di ricavare potenza attiva, reattiva e apparente erogate dal generatore di tensione e(t).
. Si chiede di scrivere e risolvere un sistema completo di equazioni di equilibrio usando il metodo dei Potenziali Nodali , e di ricavare potenza attiva, reattiva e apparente erogate dal generatore di tensione e(t).Ringrazio anticipatamente chiunque mi aiuterà nell' impresa.


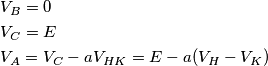
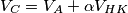 ?
?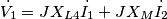
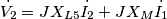
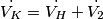
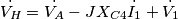

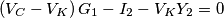
 ?
?