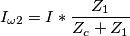Analisi circuitale in regime sinusoidale
Salve a tutti,posto uno schema circuitale su cui ho ragionato oggi,sperando di avere riscontri sul procedimento adottato;i risultati che ottengo non sono coincidenti alla perfezione con una serie di valori messi a disposizione nella soluzione per cui volevo vedere se sbaglio qualcosa in questo tipo di esercizio e dove.
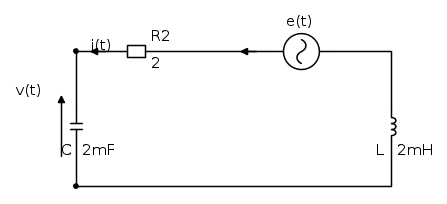
Ecco lo schema:
Anzitutto ho trasformato i generatori in fasori:

con

Poi ho proceduto,spegnengo il generatore di corrente a(t) e ho ottenuto questo circuito,in cui R1 sparisce in quanto non vi scorre corrente e in cui V(t) è la tensione ai capi del condensatore.
Essendo le impedenze in serie,per trovare V dovuta al generatore di tensione ho applicato il partitore di tensione su C:

Per la corrente invece ho calcolato l'impedenza totale

E poi ho diviso il fasore rappresentante e(t) per Z

Io per eseguire il calcolo considero il fasore come numero da risolvere,quindi mi calcolo il coseno dell'angolo e lo moltiplico per 10,a quel punto ho un numero reale diviso per un numero complesso da razionalizzare...fin qui è giusto?
Se volete posto i calcoli,perché non riesco a capire cosa sbaglio visto che i risultati non mi corrispondono per niente....
Ecco lo schema:
Anzitutto ho trasformato i generatori in fasori:

con

Poi ho proceduto,spegnengo il generatore di corrente a(t) e ho ottenuto questo circuito,in cui R1 sparisce in quanto non vi scorre corrente e in cui V(t) è la tensione ai capi del condensatore.
Essendo le impedenze in serie,per trovare V dovuta al generatore di tensione ho applicato il partitore di tensione su C:

Per la corrente invece ho calcolato l'impedenza totale

E poi ho diviso il fasore rappresentante e(t) per Z

Io per eseguire il calcolo considero il fasore come numero da risolvere,quindi mi calcolo il coseno dell'angolo e lo moltiplico per 10,a quel punto ho un numero reale diviso per un numero complesso da razionalizzare...fin qui è giusto?
Se volete posto i calcoli,perché non riesco a capire cosa sbaglio visto che i risultati non mi corrispondono per niente....

 per indicare il prodotto. In questo caso specifico non mettere nulla.
per indicare il prodotto. In questo caso specifico non mettere nulla. , diciamo piuttosto uguale al primo dei due effetti. Se chiamiamo la tensione ai capi del condensatore dovuta al solo generatore di tensione come
, diciamo piuttosto uguale al primo dei due effetti. Se chiamiamo la tensione ai capi del condensatore dovuta al solo generatore di tensione come 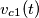 e quella ai capi del lato aperto
e quella ai capi del lato aperto 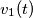 abbiamo
abbiamo 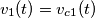 .
. ai suoi capi. Il fasore di questa si trova per esempio calcolando l'impedenza equivalente del resto del circuito e moltiplicandola per il fasore della corrente impressa dal generatore.
ai suoi capi. Il fasore di questa si trova per esempio calcolando l'impedenza equivalente del resto del circuito e moltiplicandola per il fasore della corrente impressa dal generatore. .
.
 con modulo pari a circa 8.11 e fase pari a -46.87 gradi.
con modulo pari a circa 8.11 e fase pari a -46.87 gradi.



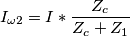
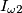 intendi la corrente nel condensatore quella formula è sbagliata. Sarebbe
intendi la corrente nel condensatore quella formula è sbagliata. Sarebbe