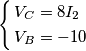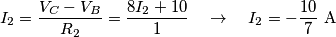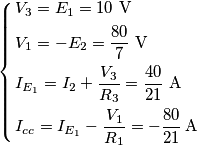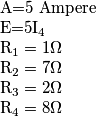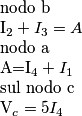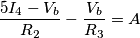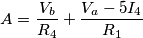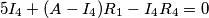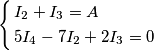Circuito con generatore pilotato,caso particolare
Ciao a tutti,porto all'attenzione un circuito in cui si presenta un caso particolare dell'applicazione dei potenziali nodali.
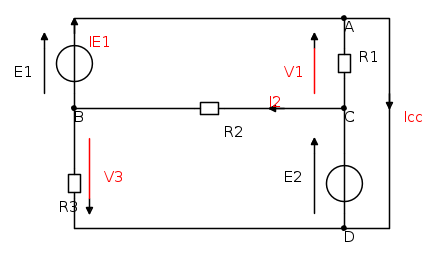
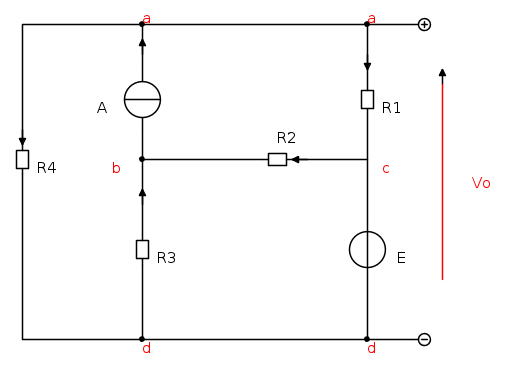
Ecco la rete:
In questa rete viene chiesto eplicitamente di trovare le seguenti grandezze:

utilizzando il metodo dei potenziali di nodo,nel caso particolare in cui il generatore E2 sia pilotato secondo la seguente funzione:

Il resto delle grandezze è:

La particolarità in questo caso sta n el fatto che uno dei potenziali di nodo,in questo caso quello al nodo c e che dovrebbe essere un potenziale noto è espresso in funzione di una corrente che sussiste sullo stesso nodo.
In questo caso come è meglio procedere?
Con l'analisi nodale normale c'è il superanello del generatore indipendente ma in questo caso è semplice,da luogo a una equazione di vincolo tra i nodi b ed a,mentre se si usa quella modificata bisognerebbe aggiungere anche le correnti dei due generatori...ho tentato con l'analisi nodale non modificata ma la presenza del legame tra Vc e I2 mi ha creato problemi,nel senso che non riesco a trovare le incognite del circuito,trovandomi con più incognite che equazioni (un'equazione per a,una per b,il potenziale c scritto in funzione di I2 e il vincolo per vb e va)
Mi spiace aver intasato il forum con tante discussioni in pochi giorni,ad ogni modo ringrazio per l'aiuto ricevuto finora,mi è stato molto utile per continuare la preparazione all'esame,che ormai è in arrivo :)
Ecco la rete:
In questa rete viene chiesto eplicitamente di trovare le seguenti grandezze:

utilizzando il metodo dei potenziali di nodo,nel caso particolare in cui il generatore E2 sia pilotato secondo la seguente funzione:

Il resto delle grandezze è:

La particolarità in questo caso sta n el fatto che uno dei potenziali di nodo,in questo caso quello al nodo c e che dovrebbe essere un potenziale noto è espresso in funzione di una corrente che sussiste sullo stesso nodo.
In questo caso come è meglio procedere?
Con l'analisi nodale normale c'è il superanello del generatore indipendente ma in questo caso è semplice,da luogo a una equazione di vincolo tra i nodi b ed a,mentre se si usa quella modificata bisognerebbe aggiungere anche le correnti dei due generatori...ho tentato con l'analisi nodale non modificata ma la presenza del legame tra Vc e I2 mi ha creato problemi,nel senso che non riesco a trovare le incognite del circuito,trovandomi con più incognite che equazioni (un'equazione per a,una per b,il potenziale c scritto in funzione di I2 e il vincolo per vb e va)
Mi spiace aver intasato il forum con tante discussioni in pochi giorni,ad ogni modo ringrazio per l'aiuto ricevuto finora,mi è stato molto utile per continuare la preparazione all'esame,che ormai è in arrivo :)