ESERCIZIO 2 - un solo generatore variabile
Segnalate errori se presenti, indicando il modo giusto per procedere, oppure se ci sono altri metodi per svolgere l'esercizio. Grazie! 
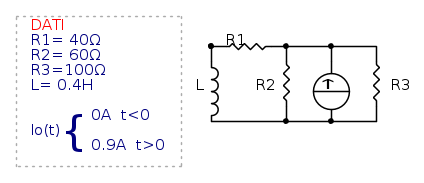
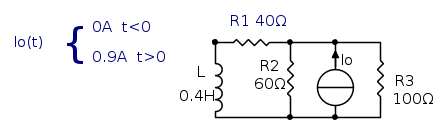
Nel circuito in figura, il generatore si accende all'istante t=0.
Determinare la corrente nell'induttore L in ogni istante di tempo.
per t<0
Il generatore di corrente è pari a zero, pertanto![\[i_{L}=0\] \[i_{L}=0\]](/forum/latexrender/pictures/8e4a1f801987071e31362ddad995d8bd.png)
per t>0
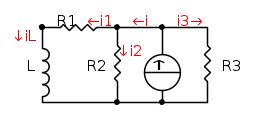
La corrente che circola in L è la stessa lungo R1, si può semplificare
![\[R_{12}=R_{1}//R_{2}=24\Omega\] \[R_{12}=R_{1}//R_{2}=24\Omega\]](/forum/latexrender/pictures/932e49e6b1103da3fa72ccc578bf5952.png)
![\[i= I_{0}\frac{R_{3}}{R_{12}+R_ {3}}=0.9\frac{100}{100+24}=0.72A\] \[i= I_{0}\frac{R_{3}}{R_{12}+R_ {3}}=0.9\frac{100}{100+24}=0.72A\]](/forum/latexrender/pictures/ce9cf4e24518f470f73e729b5b528559.png)
con la regola del partitore trovo i1
![\[i_{1}= i\frac{R_{2}}{R_{1}+R_ {2}}=0.432A\] \[i_{1}= i\frac{R_{2}}{R_{1}+R_ {2}}=0.432A\]](/forum/latexrender/pictures/71093eeda0fa228abab719e3bccc7eb4.png)
![\[{R_{eq}}=R_{1}+R_{2}=40+60=100\] \[{R_{eq}}=R_{1}+R_{2}=40+60=100\]](/forum/latexrender/pictures/aa60f45b8a7ad4a98b7316246d59d843.png)
![\[\tau =\frac{L}{R_{eq}}=\frac{0.4}{100}\] \[\tau =\frac{L}{R_{eq}}=\frac{0.4}{100}\]](/forum/latexrender/pictures/4e5152a89a465c0f62c4b2a309547e3c.png)
dove:![\[i_{L(\infty )}=i_{L}(0)+i= 0+0.432\] \[i_{L(\infty )}=i_{L}(0)+i= 0+0.432\]](/forum/latexrender/pictures/58e01a92aa5d4b575e248c520a47d346.png)
la corrente nell'induttore in ogni istante di tempo sarà:
![\[i_{L}(t)=[i_{L(0)}-i_{L(\infty )}]e^{-\frac{t}{\tau }}+i_{L(\infty )}\] \[i_{L}(t)=[i_{L(0)}-i_{L(\infty )}]e^{-\frac{t}{\tau }}+i_{L(\infty )}\]](/forum/latexrender/pictures/3cc4f02624baa19c4d6ea3ec94f7b95d.png)
![\[i_{L}(t)= (0-0.432)e^{-250t}+0.432\] \[i_{L}(t)= (0-0.432)e^{-250t}+0.432\]](/forum/latexrender/pictures/69832bbfc2f9c18b45ffccdb9599649a.png)
![\[i_{L}(t)= +0.432-0.432e^{-250t}\] \[i_{L}(t)= +0.432-0.432e^{-250t}\]](/forum/latexrender/pictures/38a60fa80e768056acd2c407f5d74b3a.png)
Oppure tramite il sistema di equazioni:
![\[\begin{cases} & \ i=i_{L}+i_{2} \\ & \ V_{2}=V_{L}+V_{1} \end{cases} \; tenendo\; conto\; che\; \; i_{L}=i_{1}\] \[\begin{cases} & \ i=i_{L}+i_{2} \\ & \ V_{2}=V_{L}+V_{1} \end{cases} \; tenendo\; conto\; che\; \; i_{L}=i_{1}\]](/forum/latexrender/pictures/0c6c8f70feb1745eb2bc79b08362289b.png)
risolvo ed ordino:
![\[V_{L}+i_{L}[R_{1}+R_{2}]=R_{2}i\] \[V_{L}+i_{L}[R_{1}+R_{2}]=R_{2}i\]](/forum/latexrender/pictures/09713ca857986dfd0e7372b426cdfe53.png)
![\[\lambda +\frac{R_{1}+R_{2}}{L}=0\; \; \Rightarrow \lambda=-250\] \[\lambda +\frac{R_{1}+R_{2}}{L}=0\; \; \Rightarrow \lambda=-250\]](/forum/latexrender/pictures/1ccba9e556a2a3da0da8387db3c205b4.png)
![\[y_{oi_{L}}=Ae^{-250t}\] \[y_{oi_{L}}=Ae^{-250t}\]](/forum/latexrender/pictures/05359a9918dbef68069cb2d5349c46fb.png)
![\[y_{pi_{L}}: \frac{(R_{1}+R_{2})}{L}B=\frac{R_{2}i}{L}\; \; \Rightarrow B=0.432\] \[y_{pi_{L}}: \frac{(R_{1}+R_{2})}{L}B=\frac{R_{2}i}{L}\; \; \Rightarrow B=0.432\]](/forum/latexrender/pictures/c63d5cdea07d36d19d8c89ba04059de1.png)
![\[y_{pi_{L}}=Ae^{-250t}+0.432\] \[y_{pi_{L}}=Ae^{-250t}+0.432\]](/forum/latexrender/pictures/147e40321fa3074859d35dac9b6c4731.png)
trovo A imponendo:
![\[i_{L}(0^{-})=i_{L}(0^{+})\] \[i_{L}(0^{-})=i_{L}(0^{+})\]](/forum/latexrender/pictures/31196e48afa3d907fbd1ef5c684d1a36.png)
![\[0= A+0.432\; \; \Rightarrow A=-0.432\] \[0= A+0.432\; \; \Rightarrow A=-0.432\]](/forum/latexrender/pictures/4f630a237174fedc69b108e19e09e342.png)
![\[i_{L}(t)=-0.432e^{-250t}+0.432\] \[i_{L}(t)=-0.432e^{-250t}+0.432\]](/forum/latexrender/pictures/f5ab3ea0a37d69432bfdca66deda72bf.png)
Nel circuito in figura, il generatore si accende all'istante t=0.
Determinare la corrente nell'induttore L in ogni istante di tempo.
per t<0
Il generatore di corrente è pari a zero, pertanto
![\[i_{L}=0\] \[i_{L}=0\]](/forum/latexrender/pictures/8e4a1f801987071e31362ddad995d8bd.png)
per t>0
La corrente che circola in L è la stessa lungo R1, si può semplificare
![\[R_{12}=R_{1}//R_{2}=24\Omega\] \[R_{12}=R_{1}//R_{2}=24\Omega\]](/forum/latexrender/pictures/932e49e6b1103da3fa72ccc578bf5952.png)
![\[i= I_{0}\frac{R_{3}}{R_{12}+R_ {3}}=0.9\frac{100}{100+24}=0.72A\] \[i= I_{0}\frac{R_{3}}{R_{12}+R_ {3}}=0.9\frac{100}{100+24}=0.72A\]](/forum/latexrender/pictures/ce9cf4e24518f470f73e729b5b528559.png)
con la regola del partitore trovo i1
![\[i_{1}= i\frac{R_{2}}{R_{1}+R_ {2}}=0.432A\] \[i_{1}= i\frac{R_{2}}{R_{1}+R_ {2}}=0.432A\]](/forum/latexrender/pictures/71093eeda0fa228abab719e3bccc7eb4.png)
![\[{R_{eq}}=R_{1}+R_{2}=40+60=100\] \[{R_{eq}}=R_{1}+R_{2}=40+60=100\]](/forum/latexrender/pictures/aa60f45b8a7ad4a98b7316246d59d843.png)
![\[\tau =\frac{L}{R_{eq}}=\frac{0.4}{100}\] \[\tau =\frac{L}{R_{eq}}=\frac{0.4}{100}\]](/forum/latexrender/pictures/4e5152a89a465c0f62c4b2a309547e3c.png)
dove:
![\[i_{L(\infty )}=i_{L}(0)+i= 0+0.432\] \[i_{L(\infty )}=i_{L}(0)+i= 0+0.432\]](/forum/latexrender/pictures/58e01a92aa5d4b575e248c520a47d346.png)
la corrente nell'induttore in ogni istante di tempo sarà:
![\[i_{L}(t)=[i_{L(0)}-i_{L(\infty )}]e^{-\frac{t}{\tau }}+i_{L(\infty )}\] \[i_{L}(t)=[i_{L(0)}-i_{L(\infty )}]e^{-\frac{t}{\tau }}+i_{L(\infty )}\]](/forum/latexrender/pictures/3cc4f02624baa19c4d6ea3ec94f7b95d.png)
![\[i_{L}(t)= (0-0.432)e^{-250t}+0.432\] \[i_{L}(t)= (0-0.432)e^{-250t}+0.432\]](/forum/latexrender/pictures/69832bbfc2f9c18b45ffccdb9599649a.png)
![\[i_{L}(t)= +0.432-0.432e^{-250t}\] \[i_{L}(t)= +0.432-0.432e^{-250t}\]](/forum/latexrender/pictures/38a60fa80e768056acd2c407f5d74b3a.png)
Oppure tramite il sistema di equazioni:
![\[\begin{cases} & \ i=i_{L}+i_{2} \\ & \ V_{2}=V_{L}+V_{1} \end{cases} \; tenendo\; conto\; che\; \; i_{L}=i_{1}\] \[\begin{cases} & \ i=i_{L}+i_{2} \\ & \ V_{2}=V_{L}+V_{1} \end{cases} \; tenendo\; conto\; che\; \; i_{L}=i_{1}\]](/forum/latexrender/pictures/0c6c8f70feb1745eb2bc79b08362289b.png)
risolvo ed ordino:
![\[V_{L}+i_{L}[R_{1}+R_{2}]=R_{2}i\] \[V_{L}+i_{L}[R_{1}+R_{2}]=R_{2}i\]](/forum/latexrender/pictures/09713ca857986dfd0e7372b426cdfe53.png)
![\[\lambda +\frac{R_{1}+R_{2}}{L}=0\; \; \Rightarrow \lambda=-250\] \[\lambda +\frac{R_{1}+R_{2}}{L}=0\; \; \Rightarrow \lambda=-250\]](/forum/latexrender/pictures/1ccba9e556a2a3da0da8387db3c205b4.png)
![\[y_{oi_{L}}=Ae^{-250t}\] \[y_{oi_{L}}=Ae^{-250t}\]](/forum/latexrender/pictures/05359a9918dbef68069cb2d5349c46fb.png)
![\[y_{pi_{L}}: \frac{(R_{1}+R_{2})}{L}B=\frac{R_{2}i}{L}\; \; \Rightarrow B=0.432\] \[y_{pi_{L}}: \frac{(R_{1}+R_{2})}{L}B=\frac{R_{2}i}{L}\; \; \Rightarrow B=0.432\]](/forum/latexrender/pictures/c63d5cdea07d36d19d8c89ba04059de1.png)
![\[y_{pi_{L}}=Ae^{-250t}+0.432\] \[y_{pi_{L}}=Ae^{-250t}+0.432\]](/forum/latexrender/pictures/147e40321fa3074859d35dac9b6c4731.png)
trovo A imponendo:
![\[i_{L}(0^{-})=i_{L}(0^{+})\] \[i_{L}(0^{-})=i_{L}(0^{+})\]](/forum/latexrender/pictures/31196e48afa3d907fbd1ef5c684d1a36.png)
![\[0= A+0.432\; \; \Rightarrow A=-0.432\] \[0= A+0.432\; \; \Rightarrow A=-0.432\]](/forum/latexrender/pictures/4f630a237174fedc69b108e19e09e342.png)
![\[i_{L}(t)=-0.432e^{-250t}+0.432\] \[i_{L}(t)=-0.432e^{-250t}+0.432\]](/forum/latexrender/pictures/f5ab3ea0a37d69432bfdca66deda72bf.png)
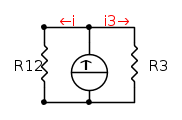
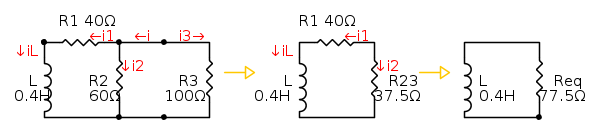
 nel calcolo della
nel calcolo della  vista dall'induttanza?
vista dall'induttanza? ,
,  e la costante di tempo
e la costante di tempo  .
.
 dove le G sono le conduttanze dei tre elementi resistivi.
dove le G sono le conduttanze dei tre elementi resistivi.

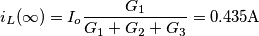
![\[i_{L}(t)= (0-0.435)e^{-250t}+0.435\] \[i_{L}(t)= (0-0.435)e^{-250t}+0.435\]](/forum/latexrender/pictures/efa7c8bf8ee0a52fa8db3ef1994cc76f.png)
![\[i_{L}(t)= +0.435-0.435e^{-250t}\] \[i_{L}(t)= +0.435-0.435e^{-250t}\]](/forum/latexrender/pictures/5439e32613707fad28855f73f1be8ba2.png)
 , continuo con il calcolare:
, continuo con il calcolare:![\[R_{23}=R_{2}//R_{3}=37.5\Omega\] \[R_{23}=R_{2}//R_{3}=37.5\Omega\]](/forum/latexrender/pictures/4798b87fabcc2f47237796dd29d8b0b3.png)
![\[i_{L}= I_{0}\frac{R_{23}}{R_{23}+R_ {1}}=0.9\frac{37.5}{37.5+40}=0.435A\] \[i_{L}= I_{0}\frac{R_{23}}{R_{23}+R_ {1}}=0.9\frac{37.5}{37.5+40}=0.435A\]](/forum/latexrender/pictures/82ae84219ab192550fcc4d54f6631c45.png)
![\[i_{L(\infty )}=i_{L}(0)+i= 0+0.435\] \[i_{L(\infty )}=i_{L}(0)+i= 0+0.435\]](/forum/latexrender/pictures/2ee439a6627b722a0f5ff6aee3dfad24.png)
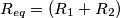 //
//