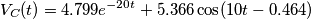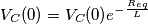ESERCIZIO 4 - aiuto, caso impedenza?
Siccome e' la prima tipologia di esercizio in cui mi imbatto, preferisco fare tutti i passaggi per comprendere da dove derivano i risultati. Ho svolto per ora solo la prima parte.
Si accettano consigli e segnalazioni errori e metodi di calcolo.
Nel circuito in figura, il generatore si spegne all’istante t=0. Determinare la tensione ai capi del condensatore in ogni istante di tempo.
Semplifico il circuito in
![\[R_{23}=R_{2}+R_{3}=40+60=100\Omega\] \[R_{23}=R_{2}+R_{3}=40+60=100\Omega\]](/forum/latexrender/pictures/d60450cb37e8d7ab7a20db5d03fc2993.png)
per t<0 ;
[unparseable or potentially dangerous latex formula]


dove:![\[Z_{C}=-\frac{j}{\omega c}=-\frac{j}{10\cdot 0.001}=-100j\] \[Z_{C}=-\frac{j}{\omega c}=-\frac{j}{10\cdot 0.001}=-100j\]](/forum/latexrender/pictures/126c8b1de1e4d858b7cffa6893b62f11.png)
![\[Z_{eq}=R_{1}+Z_{RC}=-4900-5000j\] \[Z_{eq}=R_{1}+Z_{RC}=-4900-5000j\]](/forum/latexrender/pictures/9189a1f4b571b031f8aba6e55268d423.png)
![\[V=RI\Rightarrow I=\frac{e}{Z_{eq}}=\frac{12}{(-4900-5000j)}\] \[V=RI\Rightarrow I=\frac{e}{Z_{eq}}=\frac{12}{(-4900-5000j)}\]](/forum/latexrender/pictures/e182c8d383b800afbb3c9750e490b9f1.png)
![\[I=\frac{-12(4900-5000j)}{(4900+5000j)(4900-5000j)}=\frac{-58800+60000j}{49010000}\] \[I=\frac{-12(4900-5000j)}{(4900+5000j)(4900-5000j)}=\frac{-58800+60000j}{49010000}\]](/forum/latexrender/pictures/4fe0be4fb5375fe4c9367d5c8963db51.png)
![\[I=-0.001199755+0.001224239j\] \[I=-0.001199755+0.001224239j\]](/forum/latexrender/pictures/b415586a3e40490cacf4916786369d1d.png)
Tramite il partitore posso calcolare la corrente lungo C
![\[i_{C}=I\frac{R_{23}}{R_{23}+Z_{C}}\Rightarrow (-0.001199755+0.001224239j)\frac{100}{100-100j}\] \[i_{C}=I\frac{R_{23}}{R_{23}+Z_{C}}\Rightarrow (-0.001199755+0.001224239j)\frac{100}{100-100j}\]](/forum/latexrender/pictures/2172e4157dc7c71e72487f665fad82a0.png)
![\[i_{C}=\frac{(-0.1199755+0.1224239j)(100+100j)}{(100-100j)(100+100j)}\] \[i_{C}=\frac{(-0.1199755+0.1224239j)(100+100j)}{(100-100j)(100+100j)}\]](/forum/latexrender/pictures/7c2c84a5a82e4c4a93625508455776c2.png)
![\[i_{C}=\frac{-11.99755-11.99755j+12.24239j-12.24239}{200}\] \[i_{C}=\frac{-11.99755-11.99755j+12.24239j-12.24239}{200}\]](/forum/latexrender/pictures/b3c5ce0ea382bb184c14ff3331b38a26.png)
![\[i_{C}=\frac{-24.23994+0.24484j}{200}=-0.1211997+0.0012242j\] \[i_{C}=\frac{-24.23994+0.24484j}{200}=-0.1211997+0.0012242j\]](/forum/latexrender/pictures/550a9351e35c24a3d2d402afa5aaada2.png)
![\[V_{C}=Z_{C}i_{C}=(-100j)(-0.1211997+0.0012242j)\] \[V_{C}=Z_{C}i_{C}=(-100j)(-0.1211997+0.0012242j)\]](/forum/latexrender/pictures/3c5196fcc6476d047174c79b7749c4e4.png)
![\[V_{C}=+0.12242+12.11997j\] \[V_{C}=+0.12242+12.11997j\]](/forum/latexrender/pictures/ec17c4a8b57ba1005c6b5d33e527b1c5.png)
![\[V_{m}=\sqrt{+0.12242^{2}+12.11997^{2}}=12.12058825\] \[V_{m}=\sqrt{+0.12242^{2}+12.11997^{2}}=12.12058825\]](/forum/latexrender/pictures/e7394b0ec30099ebfe561442e0d2aa9a.png)
![\[\tan \alpha =\frac{y}{x}=\frac{12.11997}{0.12242}=99.00\] \[\tan \alpha =\frac{y}{x}=\frac{12.11997}{0.12242}=99.00\]](/forum/latexrender/pictures/a8bf3baace2c4a414e949b532a4da666.png)
![\[\alpha =1.56\] \[\alpha =1.56\]](/forum/latexrender/pictures/20bb42f0bea823e646b68addaa8d3dff.png)
Sostituisco nella formula:![\[V_{C}=V_{m}e^{\alpha j}\] \[V_{C}=V_{m}e^{\alpha j}\]](/forum/latexrender/pictures/33c1cbc1e9bd28a75e441c0a1c1a735a.png)
![\[V_{C}=12.12058825\, e^{1.56 j}\] \[V_{C}=12.12058825\, e^{1.56 j}\]](/forum/latexrender/pictures/c885932e9ac4d397889941ae644f43bb.png)
che può esser scritto come![\[V_{C}=12.12058825\cos (10t+1.56)\] \[V_{C}=12.12058825\cos (10t+1.56)\]](/forum/latexrender/pictures/63dc75899278d8f827094e71adbc44e3.png)
per quanto riguarda la seconda parte, ossia per t>0
1)Considero eo=12cos(10t)V per qualunque t, mi chiedo, in questo caso non danno un contributo costante?
2)Calcolo condizioni iniziali nulle. e(t) per t=0
3)Sommo il contributo 2) con 1). Questo è il termine transitorio![\[V_{C}(\infty )\] \[V_{C}(\infty )\]](/forum/latexrender/pictures/a1c3928197833fb1688e94ac53c72b36.png) per t>0
per t>0
ASPETTO IL VOSTRO VIA PER COMPLETARE IL TUTTO. GRAZIE
Si accettano consigli e segnalazioni errori e metodi di calcolo.
Nel circuito in figura, il generatore si spegne all’istante t=0. Determinare la tensione ai capi del condensatore in ogni istante di tempo.
Semplifico il circuito in
![\[R_{23}=R_{2}+R_{3}=40+60=100\Omega\] \[R_{23}=R_{2}+R_{3}=40+60=100\Omega\]](/forum/latexrender/pictures/d60450cb37e8d7ab7a20db5d03fc2993.png)
per t<0 ;
[unparseable or potentially dangerous latex formula]


dove:
![\[Z_{C}=-\frac{j}{\omega c}=-\frac{j}{10\cdot 0.001}=-100j\] \[Z_{C}=-\frac{j}{\omega c}=-\frac{j}{10\cdot 0.001}=-100j\]](/forum/latexrender/pictures/126c8b1de1e4d858b7cffa6893b62f11.png)
![\[Z_{eq}=R_{1}+Z_{RC}=-4900-5000j\] \[Z_{eq}=R_{1}+Z_{RC}=-4900-5000j\]](/forum/latexrender/pictures/9189a1f4b571b031f8aba6e55268d423.png)
![\[V=RI\Rightarrow I=\frac{e}{Z_{eq}}=\frac{12}{(-4900-5000j)}\] \[V=RI\Rightarrow I=\frac{e}{Z_{eq}}=\frac{12}{(-4900-5000j)}\]](/forum/latexrender/pictures/e182c8d383b800afbb3c9750e490b9f1.png)
![\[I=\frac{-12(4900-5000j)}{(4900+5000j)(4900-5000j)}=\frac{-58800+60000j}{49010000}\] \[I=\frac{-12(4900-5000j)}{(4900+5000j)(4900-5000j)}=\frac{-58800+60000j}{49010000}\]](/forum/latexrender/pictures/4fe0be4fb5375fe4c9367d5c8963db51.png)
![\[I=-0.001199755+0.001224239j\] \[I=-0.001199755+0.001224239j\]](/forum/latexrender/pictures/b415586a3e40490cacf4916786369d1d.png)
Tramite il partitore posso calcolare la corrente lungo C
![\[i_{C}=I\frac{R_{23}}{R_{23}+Z_{C}}\Rightarrow (-0.001199755+0.001224239j)\frac{100}{100-100j}\] \[i_{C}=I\frac{R_{23}}{R_{23}+Z_{C}}\Rightarrow (-0.001199755+0.001224239j)\frac{100}{100-100j}\]](/forum/latexrender/pictures/2172e4157dc7c71e72487f665fad82a0.png)
![\[i_{C}=\frac{(-0.1199755+0.1224239j)(100+100j)}{(100-100j)(100+100j)}\] \[i_{C}=\frac{(-0.1199755+0.1224239j)(100+100j)}{(100-100j)(100+100j)}\]](/forum/latexrender/pictures/7c2c84a5a82e4c4a93625508455776c2.png)
![\[i_{C}=\frac{-11.99755-11.99755j+12.24239j-12.24239}{200}\] \[i_{C}=\frac{-11.99755-11.99755j+12.24239j-12.24239}{200}\]](/forum/latexrender/pictures/b3c5ce0ea382bb184c14ff3331b38a26.png)
![\[i_{C}=\frac{-24.23994+0.24484j}{200}=-0.1211997+0.0012242j\] \[i_{C}=\frac{-24.23994+0.24484j}{200}=-0.1211997+0.0012242j\]](/forum/latexrender/pictures/550a9351e35c24a3d2d402afa5aaada2.png)
![\[V_{C}=Z_{C}i_{C}=(-100j)(-0.1211997+0.0012242j)\] \[V_{C}=Z_{C}i_{C}=(-100j)(-0.1211997+0.0012242j)\]](/forum/latexrender/pictures/3c5196fcc6476d047174c79b7749c4e4.png)
![\[V_{C}=+0.12242+12.11997j\] \[V_{C}=+0.12242+12.11997j\]](/forum/latexrender/pictures/ec17c4a8b57ba1005c6b5d33e527b1c5.png)
![\[V_{m}=\sqrt{+0.12242^{2}+12.11997^{2}}=12.12058825\] \[V_{m}=\sqrt{+0.12242^{2}+12.11997^{2}}=12.12058825\]](/forum/latexrender/pictures/e7394b0ec30099ebfe561442e0d2aa9a.png)
![\[\tan \alpha =\frac{y}{x}=\frac{12.11997}{0.12242}=99.00\] \[\tan \alpha =\frac{y}{x}=\frac{12.11997}{0.12242}=99.00\]](/forum/latexrender/pictures/a8bf3baace2c4a414e949b532a4da666.png)
![\[\alpha =1.56\] \[\alpha =1.56\]](/forum/latexrender/pictures/20bb42f0bea823e646b68addaa8d3dff.png)
Sostituisco nella formula:
![\[V_{C}=V_{m}e^{\alpha j}\] \[V_{C}=V_{m}e^{\alpha j}\]](/forum/latexrender/pictures/33c1cbc1e9bd28a75e441c0a1c1a735a.png)
![\[V_{C}=12.12058825\, e^{1.56 j}\] \[V_{C}=12.12058825\, e^{1.56 j}\]](/forum/latexrender/pictures/c885932e9ac4d397889941ae644f43bb.png)
che può esser scritto come
![\[V_{C}=12.12058825\cos (10t+1.56)\] \[V_{C}=12.12058825\cos (10t+1.56)\]](/forum/latexrender/pictures/63dc75899278d8f827094e71adbc44e3.png)
per quanto riguarda la seconda parte, ossia per t>0
1)Considero eo=12cos(10t)V per qualunque t, mi chiedo, in questo caso non danno un contributo costante?
2)Calcolo condizioni iniziali nulle. e(t) per t=0
3)Sommo il contributo 2) con 1). Questo è il termine transitorio
![\[V_{C}(\infty )\] \[V_{C}(\infty )\]](/forum/latexrender/pictures/a1c3928197833fb1688e94ac53c72b36.png) per t>0
per t>0ASPETTO IL VOSTRO VIA PER COMPLETARE IL TUTTO. GRAZIE



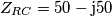


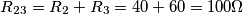
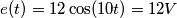

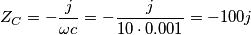
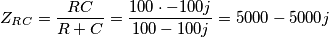
![\[Z_{eq}=R_{1}+Z_{RC}=5100-5000j\] \[Z_{eq}=R_{1}+Z_{RC}=5100-5000j\]](/forum/latexrender/pictures/44ec31dda78d969268df9b10af74926e.png)
![\[I=\frac{e}{Z_{eq}}=\frac{12}{(5100-5000j)}\] \[I=\frac{e}{Z_{eq}}=\frac{12}{(5100-5000j)}\]](/forum/latexrender/pictures/11ca0f18d88c7891ac7755963d2c1aa4.png)
![\[I=0.001199764+0.001176239j\] \[I=0.001199764+0.001176239j\]](/forum/latexrender/pictures/80e41f4077202eb6c19b54fbc22a3e0e.png)
![\[i_{C}=I\frac{R_{23}}{R_{23}+Z_{C}}\Rightarrow (0.001199764+0.001176239j)\frac{100}{100-100j}\] \[i_{C}=I\frac{R_{23}}{R_{23}+Z_{C}}\Rightarrow (0.001199764+0.001176239j)\frac{100}{100-100j}\]](/forum/latexrender/pictures/91834fd81c2dce451b28804d914610af.png)
![\[i_{C}=+0.0599882+0.05881195j\] \[i_{C}=+0.0599882+0.05881195j\]](/forum/latexrender/pictures/c28404c34e04b59d5ac967a425b899f2.png)
![\[V_{C}=+5.881195-5.99882j\] \[V_{C}=+5.881195-5.99882j\]](/forum/latexrender/pictures/d2a081a60493eb860219d34c22a07efd.png)
![\[V_{m}=\sqrt{+5.881195^{2}-5.99882^{2}}=8.40085091\] \[V_{m}=\sqrt{+5.881195^{2}-5.99882^{2}}=8.40085091\]](/forum/latexrender/pictures/6db73283606a054a42cfd233f7c45206.png)
![\[\tan \alpha =\frac{y}{x}=\frac{-5.99882}{5.881195}=-1.02\] \[\tan \alpha =\frac{y}{x}=\frac{-5.99882}{5.881195}=-1.02\]](/forum/latexrender/pictures/293e7e1a0063639bd653bb4cd9950173.png)
![\[\alpha =-0.795298921\] \[\alpha =-0.795298921\]](/forum/latexrender/pictures/176002102b325e613934ae549be64241.png)
![\[V_{C}=8.40085091\, e^{-0.79 j}\] \[V_{C}=8.40085091\, e^{-0.79 j}\]](/forum/latexrender/pictures/be59a6a269828c31b209da550cebd067.png)
![\[V_{C}=8.40085091\cos (10t-0.79)\] \[V_{C}=8.40085091\cos (10t-0.79)\]](/forum/latexrender/pictures/7adcb7fa38b03088787d3abc8e0474e3.png)
![\[V_{C}(0)=5.88V\] \[V_{C}(0)=5.88V\]](/forum/latexrender/pictures/e0471d21641c64b08e1ff262ce35864a.png)
![\[R_{eq}\] \[R_{eq}\]](/forum/latexrender/pictures/263ac4172d2a2f8c62911407a3b1cbcc.png)

![\[R_{eq}=R_{1}+R_{23}=200\Omega\] \[R_{eq}=R_{1}+R_{23}=200\Omega\]](/forum/latexrender/pictures/49e4abad4ba07e3b5e61c1fac7cf3d6d.png)
![\[V_{C}(0)=V_{C}(0)e^{-\frac{R_{eq}}{L}}\Rightarrow 5.88e^{20\cdot 10^{4}t}\] \[V_{C}(0)=V_{C}(0)e^{-\frac{R_{eq}}{L}}\Rightarrow 5.88e^{20\cdot 10^{4}t}\]](/forum/latexrender/pictures/2516a1bcacd3a17ef6ebb089bc076360.png)
![\[V_{C}(t)=\begin{cases} & \ 8.40085091\cos (10t-0.79)\;\;\;\;t<0 \\ & \ 5.88e^{20\cdot 10^{4}t}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t>0 \end{cases}\] \[V_{C}(t)=\begin{cases} & \ 8.40085091\cos (10t-0.79)\;\;\;\;t<0 \\ & \ 5.88e^{20\cdot 10^{4}t}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t>0 \end{cases}\]](/forum/latexrender/pictures/a773bbe42be1094b1fee1406ae26c3e9.png)
![\[V_{C}\] \[V_{C}\]](/forum/latexrender/pictures/de6d3f45417347cad94e74aaa4c43fb8.png) , utilizzo gli apici per distinguerli? Ho la netta impressione che non siano scritti bene.
, utilizzo gli apici per distinguerli? Ho la netta impressione che non siano scritti bene.![\[\begin{cases} & \ I=i_{C}+i_{2} \\ & \ V_{C}=V_{2} \\ & \ e(t)=V_{1}+V_{C} \end{cases}\] \[\begin{cases} & \ I=i_{C}+i_{2} \\ & \ V_{C}=V_{2} \\ & \ e(t)=V_{1}+V_{C} \end{cases}\]](/forum/latexrender/pictures/b7b4e1822a7a57ac1557ad753c5e754b.png) ho un valore
ho un valore 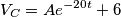
![\[\begin{array}{l}
{Z_{RC}} = \frac{{ - {\rm{j}}{X_C}R}}{{R - {\rm{j}}{X_C}}} = \frac{{100\left( { - {\rm{j}}100} \right)}}{{100 - {\rm{j}}100}} = \frac{{ - {\rm{j}}100}}{{1 - {\rm{j}}}} = \\
\\
= \frac{{ - {\rm{j}}100\left( {1 + {\rm{j}}} \right)}}{{\left( {1 - {\rm{j}}} \right)\left( {1 + {\rm{j}}} \right)}} = \frac{{ - {\rm{j}}100 + 100}}{2} = 50 - {\rm{j}}50
\end{array}\] \[\begin{array}{l}
{Z_{RC}} = \frac{{ - {\rm{j}}{X_C}R}}{{R - {\rm{j}}{X_C}}} = \frac{{100\left( { - {\rm{j}}100} \right)}}{{100 - {\rm{j}}100}} = \frac{{ - {\rm{j}}100}}{{1 - {\rm{j}}}} = \\
\\
= \frac{{ - {\rm{j}}100\left( {1 + {\rm{j}}} \right)}}{{\left( {1 - {\rm{j}}} \right)\left( {1 + {\rm{j}}} \right)}} = \frac{{ - {\rm{j}}100 + 100}}{2} = 50 - {\rm{j}}50
\end{array}\]](/forum/latexrender/pictures/294d80ed955eb79dbbe14f43a2d47071.png)
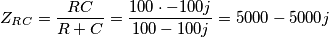

 ...rielaboro il tutto e posto (spero il giusto) e procediamo passo dopo passo!
...rielaboro il tutto e posto (spero il giusto) e procediamo passo dopo passo!
![\[Z_{RC}=\frac{R(-jx_{C})}{R-jx_{C}}=50-50j\] \[Z_{RC}=\frac{R(-jx_{C})}{R-jx_{C}}=50-50j\]](/forum/latexrender/pictures/8d32f6893f42aeb42beb458dd99c4f6b.png)
![\[Z_{eq}=R_{1}+Z_{RC}=150-50j\] \[Z_{eq}=R_{1}+Z_{RC}=150-50j\]](/forum/latexrender/pictures/9c4a62ca7eaeae36342c79e5ff63a6d7.png)
![\[I=\frac{e}{Z_{eq}}=\frac{12}{(150-50j)}=0.072+0.024j\] \[I=\frac{e}{Z_{eq}}=\frac{12}{(150-50j)}=0.072+0.024j\]](/forum/latexrender/pictures/bb88f0b003e6f80c453d11ae60444af4.png)
![\[i_{C}=I\frac{R_{23}}{R_{23}+Z_{C}}\Rightarrow (0.072+0.024j)\frac{100}{100-100j}\] \[i_{C}=I\frac{R_{23}}{R_{23}+Z_{C}}\Rightarrow (0.072+0.024j)\frac{100}{100-100j}\]](/forum/latexrender/pictures/9b1993ed1916349017232158ed415d61.png)
![\[i_{C}=0.024+0.048j\] \[i_{C}=0.024+0.048j\]](/forum/latexrender/pictures/d0e224ebd932112c2c4d63cf19ef2f94.png)
![\[V_{C}=Z_{C}i_{C}=(-100j)(0.024+0.048j)\] \[V_{C}=Z_{C}i_{C}=(-100j)(0.024+0.048j)\]](/forum/latexrender/pictures/03b63dc4d6243f35e52ddee2e124ae7e.png)
![\[V_{C}=4.8-2.4j\] \[V_{C}=4.8-2.4j\]](/forum/latexrender/pictures/c2c0a7b06a3fc1ae80baecb512ee4947.png)
![\[V_{m}=\sqrt{4.8^{2}-2.4^{2}}=5.366V\] \[V_{m}=\sqrt{4.8^{2}-2.4^{2}}=5.366V\]](/forum/latexrender/pictures/2fbee576775ca8af8b74c6051b53c2cd.png)
![\[\tan \alpha =\frac{y}{x}=\frac{-2.4}{4.8}=-0.5\] \[\tan \alpha =\frac{y}{x}=\frac{-2.4}{4.8}=-0.5\]](/forum/latexrender/pictures/8bfeb0b8b318aee96337ae7d474b5674.png)
![\[\alpha =-0.464\] \[\alpha =-0.464\]](/forum/latexrender/pictures/5837ab5ea725c6068e0c085eb021be77.png)
![\[V_{C}=5.366\, e^{-0.464 j}\] \[V_{C}=5.366\, e^{-0.464 j}\]](/forum/latexrender/pictures/76a4ec85df0d886af921beced563d5f2.png)
![\[V_{C}=5.366\cos (10t-0.464)\] \[V_{C}=5.366\cos (10t-0.464)\]](/forum/latexrender/pictures/54f5d2febc9e3f13a088a5d20bd3e4bd.png)
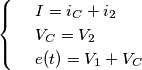
![\[R_{1}C\frac{\mathrm{d}V_{C}}{\mathrm{d} t}+V_{C}\left ( \frac{R_{1}}{R_{23}}+1 \right )=12\cos (10t)\] \[R_{1}C\frac{\mathrm{d}V_{C}}{\mathrm{d} t}+V_{C}\left ( \frac{R_{1}}{R_{23}}+1 \right )=12\cos (10t)\]](/forum/latexrender/pictures/8cf483f83ca8336c6f1151767cd3b83e.png)
![\[0.1\frac{\mathrm{d}V_{C}}{\mathrm{d} t}+2V_{C}=12\] \[0.1\frac{\mathrm{d}V_{C}}{\mathrm{d} t}+2V_{C}=12\]](/forum/latexrender/pictures/7859d238f8d34756e544f3fedcd5089b.png)
![\[\lambda +\frac{2}{0.1}=0\Rightarrow \lambda=-20\] \[\lambda +\frac{2}{0.1}=0\Rightarrow \lambda=-20\]](/forum/latexrender/pictures/4e1f2b4b5a03569bc81e860ed62e600e.png)
![\[y_{oV_{C}}=Ae^{-20t}\] \[y_{oV_{C}}=Ae^{-20t}\]](/forum/latexrender/pictures/3d4239045d4df7a1b59f143cae8b024f.png)
![\[\begin{cases} & \ y_{pV_{C'}}=B\cos\omega t+C\sin \omega t \\ & \ \[y_{pV_{C''}}=-\omega B\sin \omega t+\omega C\cos \omega t\] \end{cases}\] \[\begin{cases} & \ y_{pV_{C'}}=B\cos\omega t+C\sin \omega t \\ & \ \[y_{pV_{C''}}=-\omega B\sin \omega t+\omega C\cos \omega t\] \end{cases}\]](/forum/latexrender/pictures/536bf1b4e6ad632de25f21b89c0f0c01.png)
![\[0.1(-\omega B\sin \omega t+\omega C\cos \omega t)+2(B\cos \omega t+C\sin \omega t)=12\cos (\omega t)\] \[0.1(-\omega B\sin \omega t+\omega C\cos \omega t)+2(B\cos \omega t+C\sin \omega t)=12\cos (\omega t)\]](/forum/latexrender/pictures/047acf85d77099ade43233f2d5bbf6cc.png)
![\[\begin{cases} & \ -0.1\omega B\sin \omega t+2C\sin \omega t=0 \\ & \ 0.1\omega C\cos \omega t+2B\cos \omega t=12\cos \omega t \end{cases}\] \[\begin{cases} & \ -0.1\omega B\sin \omega t+2C\sin \omega t=0 \\ & \ 0.1\omega C\cos \omega t+2B\cos \omega t=12\cos \omega t \end{cases}\]](/forum/latexrender/pictures/0cf7d73cfe3457bf1ae25a66511c739c.png)
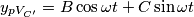 otterrò
otterrò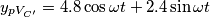
![\[\alpha \] \[\alpha \]](/forum/latexrender/pictures/f82a5d24a89352eadfbb52a84825073f.png)
 :
:![\[V_{C}(0)=4.799V\] \[V_{C}(0)=4.799V\]](/forum/latexrender/pictures/da26f30b59dc60cebb5c9ddb53419d43.png)

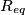
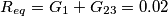
![\[V_{C}(0)=V_{C}(0)e^{-\frac{R_{eq}}{L}}\Rightarrow 4.799e^{-20t}\] \[V_{C}(0)=V_{C}(0)e^{-\frac{R_{eq}}{L}}\Rightarrow 4.799e^{-20t}\]](/forum/latexrender/pictures/b51a5b31260ecf2c2c030bf61ee49d32.png)
![\[V_{C}(t)=\begin{cases} & \ 5.366\cos (10t-0.464)\;\;\;\;t<0 \\ & \ 4.799e^{-20t}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t>0 \end{cases}\] \[V_{C}(t)=\begin{cases} & \ 5.366\cos (10t-0.464)\;\;\;\;t<0 \\ & \ 4.799e^{-20t}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t>0 \end{cases}\]](/forum/latexrender/pictures/c142e5d873559186f6cce6f5df1ec922.png)
![\[V_{C}(0^{-})=V_{C}(0^{+})\] \[V_{C}(0^{-})=V_{C}(0^{+})\]](/forum/latexrender/pictures/da536a76214a28798ea51ad29bfd5f69.png)
![\[y_{oV_{C}}=4.799e^{-20t}\] \[y_{oV_{C}}=4.799e^{-20t}\]](/forum/latexrender/pictures/ea14c3dbcfd9fcf258edc21f83ec2483.png)