Esercizio d'esame 2 - Porte
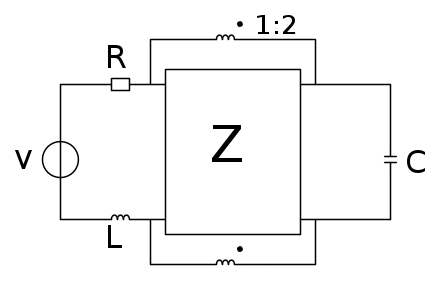
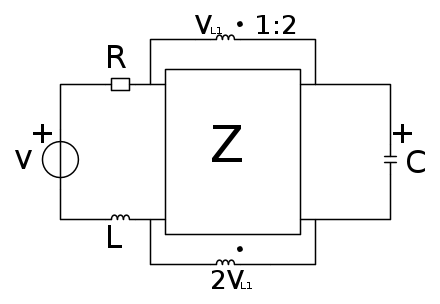
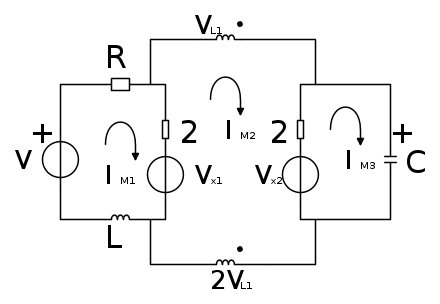
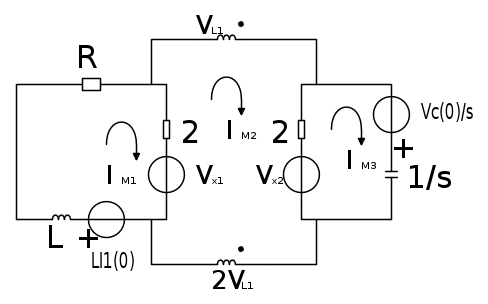
Ciao a tutti ho già postato in un altro forum (Matematicamente/Ingegneria). Si tratta di un esercizio che mi è capitato all'esame scritto di 'Teoria dei Circuiti' (Elettrotecnica per capirci, ma da 9 cfu). Vi posto lo schema fidocadj:
E i dati sono:




1) Determinare la funzione di rete che lega l'eccitazione alla risposta del circuito
alla risposta del circuito  . Dire se il circuito è stabile e in quali casi non lo è.
. Dire se il circuito è stabile e in quali casi non lo è.
2) Trovare un potenziale e
e  per tutto l'asse dei tempi.
per tutto l'asse dei tempi.
Fatemi questo favore io durante l'esame non sono riuscito a fare la (2) e non penso che mi abbia dato giusta la (1). Quindi sono sicuro di non averlo passato, comunque vi chiedo di provarci dato che non è semplice. Prima che me lo chiedete:si, quello la è un trasformatore ideale accoppiato 1:2.
E i dati sono:




1) Determinare la funzione di rete che lega l'eccitazione
 alla risposta del circuito
alla risposta del circuito  . Dire se il circuito è stabile e in quali casi non lo è.
. Dire se il circuito è stabile e in quali casi non lo è.2) Trovare un potenziale
 e
e  per tutto l'asse dei tempi.
per tutto l'asse dei tempi.Fatemi questo favore io durante l'esame non sono riuscito a fare la (2) e non penso che mi abbia dato giusta la (1). Quindi sono sicuro di non averlo passato, comunque vi chiedo di provarci dato che non è semplice. Prima che me lo chiedete:si, quello la è un trasformatore ideale accoppiato 1:2.
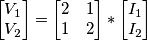
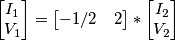
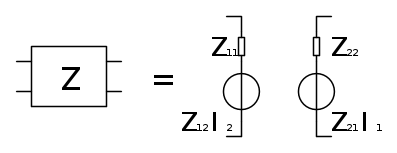
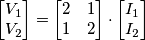
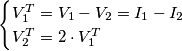
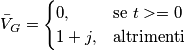
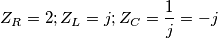
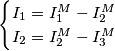
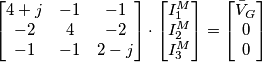
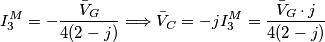
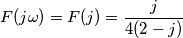

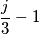 è
è 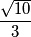 , la fase
, la fase  ho:
ho: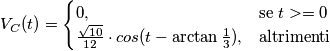

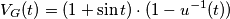
 è la funzione gradino di Heaviside.
è la funzione gradino di Heaviside.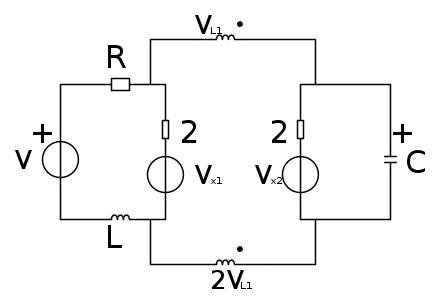
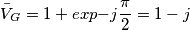
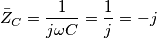

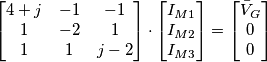
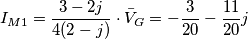
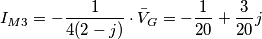
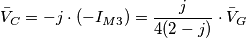
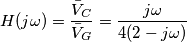
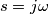 passo nel dominio di Laplace e osservo che il polo della funzione di trasferimento
passo nel dominio di Laplace e osservo che il polo della funzione di trasferimento 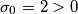 (annulla il denominatore) si trova nel semipiano destro della variabile s, dunque il circuito è di tipo instabile.
(annulla il denominatore) si trova nel semipiano destro della variabile s, dunque il circuito è di tipo instabile.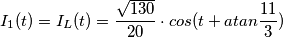
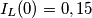
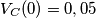
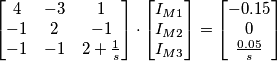






 e dice "per tutto l'asse dei tempi", intende dire di modo che possa scriversi tramite la funzione
e dice "per tutto l'asse dei tempi", intende dire di modo che possa scriversi tramite la funzione 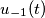 (e si intendo la funzione gradino). Si il tuo procedimento è corretto, perché il trasformatore annulla le correnti.
(e si intendo la funzione gradino). Si il tuo procedimento è corretto, perché il trasformatore annulla le correnti.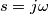 nella funzione di trasferimento (che lo stesso). Certo è preferibile usare Laplace perché viene chiesta anche la stabilità del circuito.
nella funzione di trasferimento (che lo stesso). Certo è preferibile usare Laplace perché viene chiesta anche la stabilità del circuito.