Io ho provato a risolverla così: risolvendo per variabili separabili l'equazione

si trova:

,
che pare un po' arduo scrivere nella forma
y=
y(
x) per cui conviene tenersela come
x=
x(
y); la condizione al contorno fissa la costante C al valore:

;
ora la domanda va posta in questi termini: per quale valori della costante C la funzione x(y) ha immagine non negativa? Dato che nell'intervallo
![y\in ]0,1[ y\in ]0,1[](/forum/latexrender/pictures/9ef9d32728fce399a2170be68b25a4f9.png)
la funzione x(y) è continua, e inoltre,
indipendentemente dal valore della costante C vale:

, e

, allora esiste certamente (teorema di esistenza degli zeri)
almeno un valore (diciamo che il più vicino a zero sia

) di y compreso tra 0 ed 1 per cui si ha x=0, e la funzione x(y) per valori di y compresi tra 0 e

assume tutti i possibili valori maggiori o uguali a zero, per cui l'unica condizione che la costante C deve soddisfare è esistere, il che guardando come è definita si verifica se

è diverso da 0, da +1 e da -1.
Se sbaglio spero qualcuno mi corregga perché sono curioso di sapere come va a finire. Ma quanto è bello questo forum??
 la soluzione dell'equazione :"
la soluzione dell'equazione :"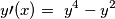 ,
, 
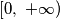 .
. la soluzione dell'equazione :"
la soluzione dell'equazione :"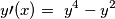 ,
, 
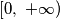 .
.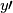
 si trova:
si trova:  ,
,  ;
;![y\in ]0,1[ y\in ]0,1[](/forum/latexrender/pictures/9ef9d32728fce399a2170be68b25a4f9.png) la funzione x(y) è continua, e inoltre,
la funzione x(y) è continua, e inoltre,  , e
, e  , allora esiste certamente (teorema di esistenza degli zeri)
, allora esiste certamente (teorema di esistenza degli zeri)  ) di y compreso tra 0 ed 1 per cui si ha x=0, e la funzione x(y) per valori di y compresi tra 0 e
) di y compreso tra 0 ed 1 per cui si ha x=0, e la funzione x(y) per valori di y compresi tra 0 e 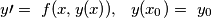
 massimale.
massimale.