Diamo i numeri 2
Dato che diamo i numeri non è ancora finito e presto parleremo della gamma di Stirling, rilassiamoci un po' con un really easy piece.

Pietro

Pietro
La comunità del mondo elettrico: elettronica, elettrotecnica, impianti, pic, plc, automazione
https://www.electroyou.it/forum/



 e verso
e verso  .
.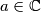
PietroBaima ha scritto:really easy piece.
PietroBaima ha scritto:la sequenza di operazioni fatta svolgere al programma.
PietroBaima ha scritto:Attento.

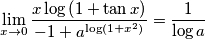
 se
se 
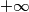 se
se 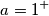
 se
se 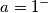
dipende dal condizionamento del problema