ElectroYou

Che differenza c'è tra i due tipi di funzioni? Non capisco perché se una funzione è Lebesgue-integrabile, può non essere Riemann-integrabile mentre se è Riemann-integrabile, è sicuramente Lebesgue-integrabile.

La definizione di integrale di Riemann per via grafica, indica la somma dell'area sottesa dai rettangolini (larghi uguali) che compongono la funzione definendo la somma superiore e inferiore di una funzione. La definizione matematica non me la ricordo non so che fine abbia fatto il quaderno di Analisi 1.

La definizione grafica di integrale di Lebesgue è simile (i rettangolini si estendono per tutta la durata della funzione, con la stessa altezza).
La definizione che mi hanno dato invece è:
$f: \mathbb{R}^n \rightarrow \mathbb{R}$ è Lebesgue integrabile se $\exists \left \{f_k\right \}_{k=1}^{\infty}$ costante a tratti tale che $f(x)=\lim_{k->+\infty}f_k(x)$ per quasi ovunque $x\in \mathbb{R}^n$ e
$\int_{\mathbb{R}^n}f(x)dx:=\lim_{k->+\infty}\int_{\mathbb{R}^n}f_k(x)dx$

Sai cos'è un funzionale lineare? Se la risposta è no non puoi capire l'integrale di Lebesgue.

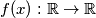Una funzione $f(x): \mathbb{R} \rightarrow \mathbb{R}$ tale per cui se 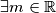$\exists m \in \mathbb{R}$ , se si incrementa

di un valore $\Delta x$ , allora f(x)

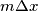incrementa di $m \Delta x$ . In genere è scritta come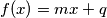 f(x)=mx+q

ok, non sai cos'è un funzionale lineare

Adesso non ho purtroppo molto tempo di spiegarmi, ma nel frattempo prova a cercare online.

Il mio intervento non c'entra niente con quello che voleva dire Pietro, ma volevo dirti una cosa che magari può tornarti utile se te la chiedano:

f(x)=mx+q

non è lineare.

Nella pratica di tutti i giorni, l'integrale di Lebesgue non serve a nulla.
Capitoli di fisica e di ingegneria si scrivono senza conoscerlo.

Quando si arriva a comprenderne il senso, che va la di là l'aver imparato definizioni e teoremi e aver passato l'esame (di Analisi 3 o 4, di metodi matematici o analisi superiore), si fa un gran passo avanti nella comprensione della matematica moderna.

Sapevo che era quella la definizione di funzione lineare. Sono aperto a chiarimenti. Su internet ho trovato quella come definizione. Ovunque.
Andando avanti in matematica mi sembra di vedere tante cose buttate li...Specie sto integrale di Lebesgue...
Immagino che non serva a niente, come metà delle cose che si imparano all'università, ma purtroppo devo impararlo.

Non ti è stato detto che non serve a niente.

Per quanto riguarda la giusta osservazione di

Ianero, prova ad applicare la definizione di linearità.
Sono certo che avrai una sorpresa.

Sei sicuro di non aver trovato la definizione di linearità affine?

Ho trovato definizioni uguali a questa
https://users.dimi.uniud.it/~paolo.bait ... elem10.pdf
per le funzioni lineari e affini.
O intendi la definizione di linearità di funzioni tipo
$f(\alpha x_1+ \beta x_2)=\alpha f(x_1)+ \beta f(x_2)$ ?

Shika93 ha scritto:O intendi...?

Quella è la definizione di linearità generale per una qualsiasi funzione (non solo quelle che operano su numeri).

Ho trovato definizioni uguali a questa

No, manca il

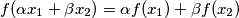(e deve mancare).

ElectroYou

Differenza funzioni integrabili secondo Riemann e Lebesgue

Differenza funzioni integrabili secondo Riemann e Lebesgue

Re: Differenza funzioni integrabili secondo Riemann e Lebesg

Re: Differenza funzioni integrabili secondo Riemann e Lebesg

Re: Differenza funzioni integrabili secondo Riemann e Lebesg

Re: Differenza funzioni integrabili secondo Riemann e Lebesg

Re: Differenza funzioni integrabili secondo Riemann e Lebesg

Re: Differenza funzioni integrabili secondo Riemann e Lebesg

Re: Differenza funzioni integrabili secondo Riemann e Lebesg

Re: Differenza funzioni integrabili secondo Riemann e Lebesg

Re: Differenza funzioni integrabili secondo Riemann e Lebesg