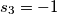[stabilire la stabilita' del sistema con la tabella di Routh
Inviato: 15 gen 2019, 13:39
Buongiorno .
Ho risposto a questa domanda :
Quale polinomio genera la seguente tabella di Routh ?



A questa domanda credo di aver risposto bene :
La risposta giusta e la b) .
Applicando la formula per determinale la tabella di Routh e' stato facile .
Sono andato avanti e mediante la regola di Rufini ho calcolato le radici del polinomio di terzo grado .
Anche qui e' stato abbastanza facile .
Le radici sono :

Il problema mi si presenta in questo punto :
Domanda : Il sistema associato alla tabella di Routh a questa domanda risulta essere :
a) Stabile
b) instabile
c) non si puo' dire nulla riguardo alla proprietà della stabilità .
Non riesco a stabilire se ci siano o no variazioni di segno
A me verrebbe da dire la c) pero' la butto li ...
Mi aiutate per favore .. Grazie.
Ho risposto a questa domanda :
Quale polinomio genera la seguente tabella di Routh ?



A questa domanda credo di aver risposto bene :
La risposta giusta e la b) .
Applicando la formula per determinale la tabella di Routh e' stato facile .
Sono andato avanti e mediante la regola di Rufini ho calcolato le radici del polinomio di terzo grado .
Anche qui e' stato abbastanza facile .
Le radici sono :

Il problema mi si presenta in questo punto :
Domanda : Il sistema associato alla tabella di Routh a questa domanda risulta essere :
a) Stabile
b) instabile
c) non si puo' dire nulla riguardo alla proprietà della stabilità .
Non riesco a stabilire se ci siano o no variazioni di segno
A me verrebbe da dire la c) pero' la butto li ...
Mi aiutate per favore .. Grazie.
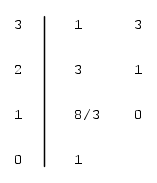



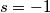 ....sbaglio ?
....sbaglio ?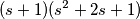
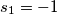 ,
, 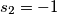 ,
,