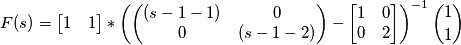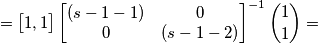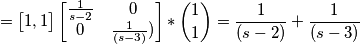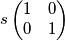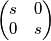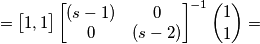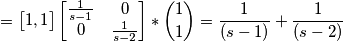[Esercizio su funzione di trasferimento]
Inviato: 23 gen 2019, 14:11
Buongiorno.
Ringrazio chi ha bloccato il post che avevo pubblicato qualche giorno fa.
Non conoscevo le funzioni e le opportunità che laTex aveva.
Conoscevo solo qualche comando. Adesso che ho iniziato ad avere piu' dimestichezza con laTex sono contento. Faccio del tutto per mantenere questa linea ed utilizzare sempre LaTex e fidocad
 )
)
A parte questa premessa .
Propongo nuovamente l'esercizio
Dato il sistema :


con

Vaerificare l'equazione fondamentale che risulta alla base del criterio di Nyquist , ovvero che vale la relazione :

Ho provato a svolgerlo in questo modo :



Tralascio qualche calcolo e la F(s) risulta :

Eseguo l'uguaglianza e arrivo a:

A questo punto mi perdo e non so andare avanti .
Cosa ne pensate ? fin qui secondo voi e' gisuto ? Grazie.
Ringrazio chi ha bloccato il post che avevo pubblicato qualche giorno fa.
Non conoscevo le funzioni e le opportunità che laTex aveva.
Conoscevo solo qualche comando. Adesso che ho iniziato ad avere piu' dimestichezza con laTex sono contento. Faccio del tutto per mantenere questa linea ed utilizzare sempre LaTex e fidocad
A parte questa premessa .
Propongo nuovamente l'esercizio
Dato il sistema :


con


Vaerificare l'equazione fondamentale che risulta alla base del criterio di Nyquist , ovvero che vale la relazione :

Ho provato a svolgerlo in questo modo :



Tralascio qualche calcolo e la F(s) risulta :

Eseguo l'uguaglianza e arrivo a:

A questo punto mi perdo e non so andare avanti .

Cosa ne pensate ? fin qui secondo voi e' gisuto ? Grazie.