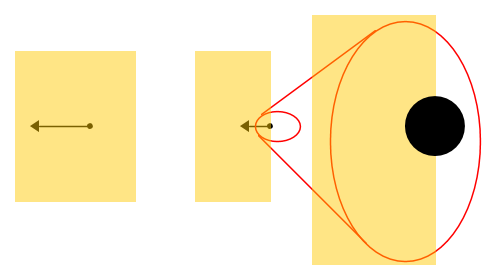
Premetto che questo esercizio l'ho visto proposto in questo forum solo che non c'è una conferma circa la sua risoluzione.
il problema è:
Un condensatore a facce piane e parallele (S=10 mm2) da 100 pF viene collegato ad una sorgente di forza elettromotrice ε=50 V; Calcolare la forza necessaria per tenere in equilibrio le armature del condensatore.
io ho agito senza tirare in ballo l'energia.
Per prima cosa ho calcolato la distanza d tra le armature del condensatore attraverso la formula della capacità.
quindi sapendo questa distanza ho calcolato il campo elettrico tra le armature del condensatore attraverso la relazione E=ε/d
quindi ho calcolato la carica presente sulle armature attraverso Q=C*V.
E poi semplicemente ho fatto F= Q*E.
Personalmente ho il presentimento che non sia il modo corretto di procedere.
Spero qualcuno mi confermi o mi smentisca.
Grazie in anticipo a tutti

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

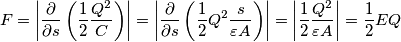



 instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.

 sulle armature è costante. L'energia immagazzinata sul condensatore è
sulle armature è costante. L'energia immagazzinata sul condensatore è
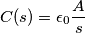 .
.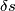 , dovrei applicare all'armatura una forza
, dovrei applicare all'armatura una forza 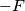 , dove
, dove  è la forza tra le armature del condensatore (o, meglio, visto che siamo in un problema scalare, la componente lungo l'asse
è la forza tra le armature del condensatore (o, meglio, visto che siamo in un problema scalare, la componente lungo l'asse  di tale forza).
di tale forza).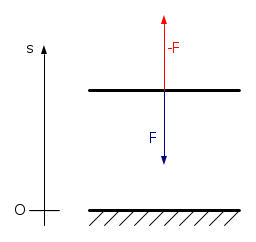
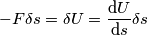
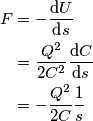
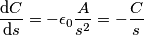
 .
.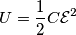
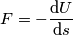
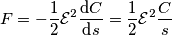
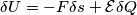
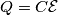 ,
, 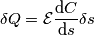
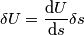
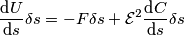

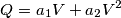 )?
)?