"
Due cariche
 e
e  nel vuoto sono fisse nello spazio ad una distanza
nel vuoto sono fisse nello spazio ad una distanza  l'una dall'altra. Si aggiunge in un punto qualsiasi una terza carica
l'una dall'altra. Si aggiunge in un punto qualsiasi una terza carica  , e massa
, e massa  con velocità nulla, libera di muoversi.
con velocità nulla, libera di muoversi.(A) Determinare il punto in cui la carica
 rimane ferma.
rimane ferma.(B) La carica
 è inizialmente posta, con velocità nulla, in posizione allineata con
è inizialmente posta, con velocità nulla, in posizione allineata con  e
e  , a una distanza
, a una distanza  da
da  e
e  da
da  . Calcolare la velocità di
. Calcolare la velocità di  quando raggiunge il punto a distanza
quando raggiunge il punto a distanza  da
da  .
."
Appena l'ho letto mi è sorto il dubbio su come considerare la forza di gravità, essendo le cariche disposte in un qualunque modo; potrebbero essere disposte sia in orizzontale, sia in verticale. Allora ho pensato che forse si intende uno spazio vuoto senza gravità. Ho provato a eguagliare le forze e trovare "il punto in cui
 rimane ferma" (anche se in realtà me ne aspetto più di uno).
rimane ferma" (anche se in realtà me ne aspetto più di uno).Il problema che è sorto è che mi esce un'equazione che non sono in grado di risolvere. Ho provato anche solo in 2 dimensioni, ma è comunque difficile e questo è uno solo dei 4 esercizi d'esame, quindi il tempo è limitato.


Quest'equazione che svolgendola mi risulta di terzo grado, andrebbe fatta anche per y e, nel caso di considerare 3 dimensioni, per z. Esiste un modo alternativo? Ho pensato anche al potenziale per diminuire il grado dell'equazione, ma non saprei come impostare il problema, anche perché non devo trovare tutte le superfici equipotenziali, ma quella in cui
 .
.
 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



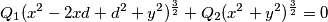
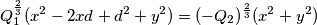
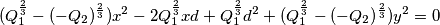
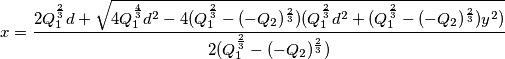
 , quindi un punto si trova facilmente.
, quindi un punto si trova facilmente.