 da
da  Peternek » 5 lug 2018, 17:36
Peternek » 5 lug 2018, 17:36
Grazie a tutti per le risposte

. In effetti come dice rugweri io di questa materia non capisco niente

e tra l'altro in questo caso stavo svolgendo per esercizio il compito di una materia parallela simile quindi non so se magari loro hanno fatto qualcosa in più o usano delle convenzioni tipo "
negli algoritmi per le potenze consideriamo il tempo necessario 
" come standard così magari non ci sarà quello che la considera O(1) per abitudine da certe librerie math di certi linguaggi oppure quello che se la calcola con un ciclo for in O(k). Ma è solo una mia ipotesi e fantasia quindi vi chiedo di non criticarmi:
per questo vi ho scritto qua, nel dubbio che non fossero fesserie e che magari non ci fossero algoritmi con prestazioni molto migliori rispetto a

che si usano solitamente.
Fatto sta che non dovrebbero aver studiato i compilatori o i riferimenti a come lo farebbe un compilatore concreto ad esempio quello di java (credo), ma anche se l'avessero fatto: mi avete già detto abbastanza vi ringrazio credo che considerino come prestazioni proprio l'algoritmo del tempo logaritmico
 con un
con un  fissato, dice che sarebbe necessario un tempo
fissato, dice che sarebbe necessario un tempo  per calcolarla.
per calcolarla.  senza chiedermi quanto ci impiega la macchina, sperando che il tempo sia bassissimo. In realtà non so quanto ci impiegano,
senza chiedermi quanto ci impiega la macchina, sperando che il tempo sia bassissimo. In realtà non so quanto ci impiegano,  sarebbe diciamo il classico tempo necessario n queste situazioni, o quello che si usa per convenzione negli algoritmi?
sarebbe diciamo il classico tempo necessario n queste situazioni, o quello che si usa per convenzione negli algoritmi?
 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)







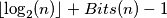 (dove
(dove 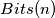 è ovviamente il numero di bit dell'esponente
è ovviamente il numero di bit dell'esponente 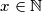 e qualsiasi esponente
e qualsiasi esponente 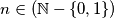 , anche se non è detto che sia sempre ottimo.
, anche se non è detto che sia sempre ottimo.