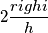Cerco il vostro aiuto in merito ad un problema spiegato nel titolo.
Premetto che: ho ben capito il concetto di capacità di un conduttore isolato, ho ben capito il problema del "sistema di conduttori" e relative matrici dei coefficienti di potenziale e dei coefficienti di capacità ed induzione.
Il problema è questo:
Si considerano n conduttori (ad es:3) cilindrici di lunghezza infinita (di raggio come vedremo piccolo rispetto alle altre grandezze geometriche) sulle cui superfici sono distribuite le cariche
 per unità di lunghezza, posti ad una certa altezza rispetto al terreno. La permettività del terreno è
per unità di lunghezza, posti ad una certa altezza rispetto al terreno. La permettività del terreno è  dell'aria che circonda i conduttori. Dunque volendo usare ad esempio il metodo delle cariche immagini per calcolare potenziale e campo elettrico sappiamo che (viste le permittività) la superficie del terreno è equipotenziale o meglio approssimabile come equipotenziale, ed il campo è ortogonale alla sup stessa.
dell'aria che circonda i conduttori. Dunque volendo usare ad esempio il metodo delle cariche immagini per calcolare potenziale e campo elettrico sappiamo che (viste le permittività) la superficie del terreno è equipotenziale o meglio approssimabile come equipotenziale, ed il campo è ortogonale alla sup stessa.La sup di separazione aria terreno è scelta a potenziale nullo.
Il potenziale nel generico punto P del semispazio superiore può essere calcolato mediante il principio di sovrapposizione degli effetti:
 in cui
in cui  è il potenziale in P dovuto alla generica coppia di conduttori costituita dal conduttore i e dalla sua immagine i':
è il potenziale in P dovuto alla generica coppia di conduttori costituita dal conduttore i e dalla sua immagine i': dove
dove  ed
ed  sono le distanze da P del conduttore i e della sua immagine i'.
sono le distanze da P del conduttore i e della sua immagine i'.Se si pone il punto del calcolo sulla superficie del conduttore 1 ad es, abbiamo:
 avendo assunto
avendo assunto  ed avendo indicato con
ed avendo indicato con  e
e  rispettivamente le distanze tra il conduttore i ed il conduttore j e tra il conduttore i ed il conduttore j' immagine di j.....(che fatica)
rispettivamente le distanze tra il conduttore i ed il conduttore j e tra il conduttore i ed il conduttore j' immagine di j.....(che fatica)Calcolando il potenziale degli altri conduttori si perviene al seguente sistema di equazioni lineari:
con i coefficienti di potenziale dati da:
 e
e
in forma matriciale:
![[V]=[A][Q'] [V]=[A][Q']](/forum/latexrender/pictures/1594d06b0c58935d1bcd0c45eb46d900.png) che può essere invertito risolvendo rispetto a Q'
che può essere invertito risolvendo rispetto a Q' ![[Q']=[A^{-1}][V]=[B][V] [Q']=[A^{-1}][V]=[B][V]](/forum/latexrender/pictures/66c9d31121e9d1fd5b434a426f605cc6.png) .
.consideriamo l'i-esima equazione

e aggiungiamo e togliamo la quantità
 escludendo il termine
escludendo il termine  otteniamo
otteniamo
Si definisce ora: capacità parziale propria dell'i-esimo conduttore la quantità:
 mentre le capacità mutue tra i vari conduttori sono
mentre le capacità mutue tra i vari conduttori sono  .
.Possiamo quindi scrivere:

La rete capacitiva è dunque nel caso di 3 conduttori:
ORA:
1) cosa significa rete capacitiva equivalente? Equivalente perché?
2)perché le seconde armature di
 sono collegate a terra che è un dielettrico??
sono collegate a terra che è un dielettrico??3) perché su nessun libro esiste questo argomento?
4)ho provato a fare da solo il caso di due sfere concentriche senza dielettrico, esempio facilissimo, ma che non coincide con i risultati noti(dopo lo posto).
5) se avete letto fin qui avete troppa pazienza

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



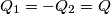 )
)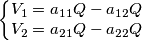
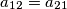
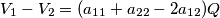 da cui
da cui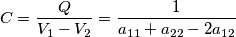
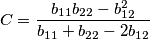
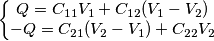
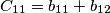
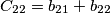
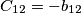 .
.