No, si dice thank you one more time, non another time

La questione del guadagno di modo comune e differenziale e` importante, e` il cuore degli amplificatori differenziali e da strumentazione, meglio trattarla in dettaglio. Se avessi studiato un po' di algebra lineare e spazi vettoriali sarebbe molto piu` semplice. Sappi che ti aspettano al varco quando sarai all'universita`.
Prendiamo un circuito lineare con due ingressi e una uscita,

. Essendo lineare, puo` solo essere del tipo

Ho messo il segno negativo ad

cosi` dopo ci si ritrova, ma ci sono anche altre analisi senza segno meno esplicito.
(Aperta parentesi: una espressione del tipo
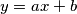 non
non e` lineare, al piu` la si puo` definire lineare affine

. Per questa ragione l'espressione di prima che ho assunto lineare non puo` avere un termine costante.)
Quando si usa un amplificatore
differenziale si e` interessati alla
differenza delle due tensioni di ingresso, differenza che porta l'informazione utile. Il valore assoluto di ciascuna delle due tensioni invece non solo non porta inormazione, ma potrebbe essere dannoso. Se si scrive il guadagno dell'ampli differenziale in questo modo

aggiungendo magari che deve essere

non si da` molta informazione in piu` su come funziona bene o male l'ampli differenziale.
Al posto di usare

e

, ciascuna moltiplicata per la propria costante, e` molto piu` significativo mettere in evidenza l fatto che la differenza di tensione fra

e

e` la quantita` importante, quantita` che chiamiamo tensione differenziale

.
Non possiamo semplicemente buttare via

e

e usare solo

perche' stiamo perdendo una dimensione: siamo partiti da due tensioni e ne abbiamo solo una: questa non e` una rappresentazione equivalente.
Dobbiamo introdurre una seconda tensione, detta tensione di modo comune

definita in questo modo:

. In pratica

e` la media fra le tensioni

e

.
Rappresentare un sistema di tensioni usando

e

oppure

e

e` la stessa cosa, si rappresenta sempre la stessa situazione. Il vantaggio e` che

e

sono facili da misurare, mentre

e

sono significative perche' mostrano il termine importante, quello che porta informazione

e quello rompiscatole

.
Dal punto di vista matematico questo e` un cambiamento di base in uno spazio vettoriale!
Date

e

si trovano

e

con le formule viste sopra (differenza e media), mentre date

e

si torna a

e

in questo modo:

mentre le altre sono

Esempio (ufficio lavori inutili, solo per verifica), se prendiamo

otteniamo

e per il modo comune

. Se prendiamo queste due tensioni e le mettiamo nelle due equazioni di sinistra, riotteniamo

e

. Abbiamo solo un'altra rappresentazione (utile) dello stesso sistema di tensioni. Utile perche' sono rappresentati in modo esplicito sia il segnale utile

che quello rompiscatole

.
Andiamo a sostituire le espressioni di

e

nell'equazione del guadagno dell'amplificatore e mettiamo in evidenza

e


In questo modo si vede quanto e` amplificato il segnale differeziale e quando il segnale comune. Si puo` scrivere

dove si e` definito

OK, ci siamo: abbiamo il guadagno di modo differenziale e quello di modo comune. Se, come si spera,

il guadagno differenziale vale

mentre quello di modo comune vale

. In effetti l'amplificatore differenziale lo si utilizza proprio per non sentire il modo comune e amplificare invece di una quantita`
nota e stabile il modo differenziale.
Peccato pero` che

e

non siano proprio identici, e quindi avremo errori su

e su

. Calcoliamo prima queste due grandezze in funzione delle resistenze e poi ci facciamo su i conti. Faccio riferimento al mio schema che ha dei nomi umani per le resistenze. I valori vedremo dopo che non sono importanti.
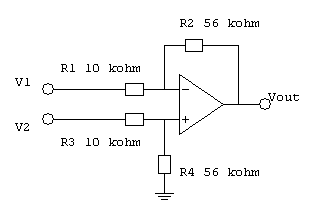
- Ampli Sensitivity1.gif (1.47 KiB) Osservato 13696 volte
I valori dei guadagni

e

sono:

e per

e

si ha invece

Da notare che il guadagno

non ha il segno negativo in quanto l'avevo gia` messo esplicitamente in evidenza nella definizione iniziale del guadagno.
Se si riuscisse a fare

e

(o anche solo

e

, con

una costante qualunque) si avrebbe

e

. Purtroppo questo non capita per due motivi almeno: le resistenze hanno una certa tolleranza relativa

e
in serie a  e
e  c'e` la resistenza interna della sorgente che puo` provocare danni
c'e` la resistenza interna della sorgente che puo` provocare danni cambiando il valore effettivo delle resistenze di ingresso dell'amplificatore differenzaie. Per questa ragione gli amplificatori differenziali e da strumentazione hanno spessissimo dei buffer (o qualcosa di piu` complicato) davanti. Le resistenze del differenziale sono "sacre" non devono essere disturbate.
Calcoliamo adesso la sensitivity dei guadagni rispetto alle variazioni delle resistenze (e questo era il quesito originario). Le resistenze sono caratterizzate da una variazione percentuale, e quindi e` naturale considerare le loro variazioni relativa. Anche per il guadagno differenziale e` una buona scelta utilizzare la variazione relativa. Dobbiamo trovare cioe` la relative sensitivity di

rispetto alle quattro resistenze. Il metodo per calcolare la relative sensitivity e` nel post precedente:

Al posto della generica

che ho indicato bisogna ripeterli per le quattro resistenze (Una noia disumana fare tutti questi conti, per fortuna che ci sono i programmi di manipolazione simbolica delle espressioni). Le derivate e i guadagni devono essere calcolati con i valori nominali delle resistenze. Questo significa che
prima si fanno i conti con
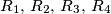 poi
poi si reintroduce la condizione che

e che

I risultati sono questi (se non ho sbagliato i conti)
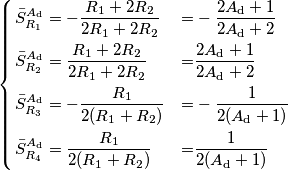 Vorsicht!
Vorsicht!: dietro questi risultati c'e`
tanta algebra: semplice ma
tanta!
Vediamo ora di calcolare le sensitivities per il guadagno di modo comune

. In questo caso le resistenze hanno sempre una variazione relativa, ma non si puo` calcolare la variazione relativa di

perche' il suo valore nominale e` zero! Se una grandezza passa da 0 a un valore anche piccolissimo, la sua variazione relativa e` infinita. Per

e` necessario (e anche piu` sensato) calcolare la variazione assoluta.
Si deve quindi usare la sensibilita` semirelativa, definita in questo modo:

, al solito valutata per le quattro diverse resistenze. Da osservare che anche questa sensitivity e` adimensionata. I risultati sono (con il solito pacco di algebra, sempre se non ho sbagliato i conti)

E` fatta, questi sono i risultati! Adesso comincia la parte difficile: che cosa vogliono dire? Cominciamo con il guadagno differenziale, che era quello che ti interessava. Guardiamo i segni

e

sono negativi: se

e

aumentano il guadagno differenziale diminuisce. Invece

e

sono positive: se

e

diminuiscono, il guadagno diminuisce.
Se vogliamo calcolare la massima variazione del guadagno differenziale

dobbiamo considerare che

e

aumentino e

e

diminuiscano. Poi consideriamo che tutte le resistenze cambino della stessa percentuale

:

E questo e` il risultato che cercavi: se le resistenze sono all'1% nel caso piu` sfortunato la variazione del guadagno e` del
2%!
Ma c'e` un altro risultato ancora piu` importante, ed e` quello del guadagno di modo comune

, che da 0 diventa diverso da zero. La sua variazione si calcola come prima, questa volta bisogna pero` supporre che ad esempio

e

aumentino e

e

diminuiscano. Seguendo la stessa procedura di prima si ottiene:

Se

e` abbastanza piu` grande di 1, con le resistenze all'1% si ottiene

e questo potrebbe essere un grosso guaio.
Supponiamo di voler misurare una caduta di tensione di 80mV su una resistenza di shunt, e di voler trasformare questa caduta di tensione in una tensione di 4V per mandarla all'A/D di un micro. Supponiamo che che questa resistenza sia collegata sul positivo dell'alimentazione a 12V. Abbiamo

. Ci serve un guadagno differenziale

e se facciamo le cose per bene il guadagno di modo comune

dovrebbe venire nullo.
Realizziamo l'amplificatore con resistori all'1%, quindi

Quali sono gli effetti sull'amplificatore? Sappiamo che al massimo

puo` cambiare del 2%, quindi il guadagno potra` variare da 49 a 51 e la lettura sara` errata al max del 2%.
Adesso pero` arriva il guaio: quale sara` la tensione in uscita dall'amplificatore? Riprendiamo l'equazione che fornisce la tensione di uscita in funzione delle grandezze di modo differenziale e di modo comune e sostituiamo i numeri:
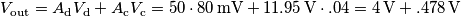
URCA! Il modo comune, a causa del resistor mismatch, raggiunge l'uscita e puo` dare un errore, in questo caso, del 12%. In realta` il modo comune, non abbastanza attenuato dall'amplificatore differenziale, da` in uscita un errore costante (un offset) che puo` arrivare a 478mV!
In un amplificatore differenziale o da strumentazione e` importante il valore del guadagno differenziale, perche' e` quello che trasforma la grandezza sentita nel sistema in grandezza misurata dal processore (o chi per lui), ma e` ancora
piu` importante che il guadagno di modo comune rimanga praticamente a zero.
Il parametro che indica quanto e` buono un amplificatore differenziale e` il Common Mode Rejection Ratio, CMRR definito in questo modo

. Nell'esempio fatto, si ha

. Gli amplificatori da strumentazione integrati arrivano oltre al centinaio di decibel.
I conti approssimati delle sensitivities un'altra volta!

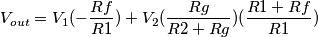
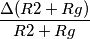 ):
):![\frac{\Delta V_{out}}{V_{out}}=\frac{\Delta (-\frac{Rf}{R1})}{(-\frac{Rf}{R1})}+\frac{\Delta [(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})]}{(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})} \frac{\Delta V_{out}}{V_{out}}=\frac{\Delta (-\frac{Rf}{R1})}{(-\frac{Rf}{R1})}+\frac{\Delta [(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})]}{(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})}](/forum/latexrender/pictures/c572b14e1a689d602192811e5b35bdc7.png)
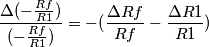
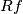 sia
sia 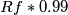 (1% in -) ed
(1% in -) ed  sia
sia 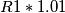 (1% in +), trovando il seguente risultato:
(1% in +), trovando il seguente risultato: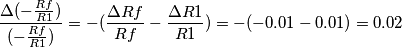
![\frac{\Delta [(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})]}{(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})}=\frac{\Delta (\frac{Rg}{R2+Rg})}{(\frac{Rg}{R2+Rg})}+\frac{\Delta (\frac{R1+Rf}{R1})}{(\frac{R1+Rf}{R1})} \frac{\Delta [(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})]}{(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})}=\frac{\Delta (\frac{Rg}{R2+Rg})}{(\frac{Rg}{R2+Rg})}+\frac{\Delta (\frac{R1+Rf}{R1})}{(\frac{R1+Rf}{R1})}](/forum/latexrender/pictures/15019107c5e34ffc72469c60423eee23.png)

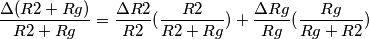
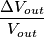 , che e' anch' essa il risultato di una somma algebrica. Tuttavia ho rimosso i termini (come faro' anche qui) perche' questi ultimi NON potranno MAI essere maggiori di 1, quindi considerandoli 1 sto considerando la worst-case-condition (right?).
, che e' anch' essa il risultato di una somma algebrica. Tuttavia ho rimosso i termini (come faro' anche qui) perche' questi ultimi NON potranno MAI essere maggiori di 1, quindi considerandoli 1 sto considerando la worst-case-condition (right?).
 puo' anche essere considerato come
puo' anche essere considerato come 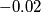 (basta che ambedue i resistori diminuiscano dell' 1% anziche' aumentare come precedentemente assunto), di conseguenza:
(basta che ambedue i resistori diminuiscano dell' 1% anziche' aumentare come precedentemente assunto), di conseguenza: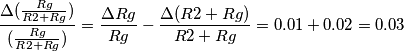
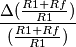 si arriva al medesimo risultato:
si arriva al medesimo risultato: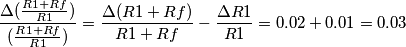
![\frac{\Delta [(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})]}{(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})}=\frac{\Delta (\frac{Rg}{R2+Rg})}{(\frac{Rg}{R2+Rg})}+\frac{\Delta (\frac{R1+Rf}{R1})}{(\frac{R1+Rf}{R1})}=0.03+0.03=0.06 \frac{\Delta [(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})]}{(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})}=\frac{\Delta (\frac{Rg}{R2+Rg})}{(\frac{Rg}{R2+Rg})}+\frac{\Delta (\frac{R1+Rf}{R1})}{(\frac{R1+Rf}{R1})}=0.03+0.03=0.06](/forum/latexrender/pictures/a3f19a82eb251cffa6c98802934a818d.png)
![\frac{\Delta V_{out}}{V_{out}}=\frac{\Delta (-\frac{Rf}{R1})}{(-\frac{Rf}{R1})}+\frac{\Delta [(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})]}{(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})}=0.06+0.02=0.08 \frac{\Delta V_{out}}{V_{out}}=\frac{\Delta (-\frac{Rf}{R1})}{(-\frac{Rf}{R1})}+\frac{\Delta [(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})]}{(\frac{Rg}{R2+Rg})(\frac{R1+Rf}{R1})}=0.06+0.02=0.08](/forum/latexrender/pictures/39bfbb821d3cf52e60ef3edf805da5bf.png)
 dell' 8%.
dell' 8%.
 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



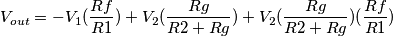
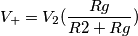
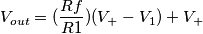
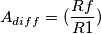
 toh, potrebbe essere una amplificazione che dipende dal valore di resistenze. Vogliamo trovare di quanto varia
toh, potrebbe essere una amplificazione che dipende dal valore di resistenze. Vogliamo trovare di quanto varia  al variare di ciascuna di quelle resistenze. Vogliamo trovare un legame fra la variazione di
al variare di ciascuna di quelle resistenze. Vogliamo trovare un legame fra la variazione di  .
. 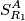 che significa la sensibilita` di
che significa la sensibilita` di  . Le variazioni di
. Le variazioni di 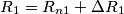 , dove
, dove 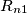 e` il valore nominale di
e` il valore nominale di 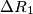 e` la variazione assoluta di
e` la variazione assoluta di  in questo caso
in questo caso  e` la variazione relativa (anche detta percentuale) di
e` la variazione relativa (anche detta percentuale) di 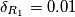 .
.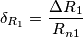
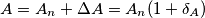
 di un transistore bipolare vengono date di solito in valore assoluto: ad esempio
di un transistore bipolare vengono date di solito in valore assoluto: ad esempio  .
.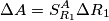 . Il valore della sensitivity e` dato da
. Il valore della sensitivity e` dato da 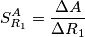
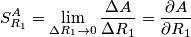 .
. si misura nelle unita` di misura di
si misura nelle unita` di misura di 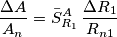
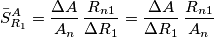
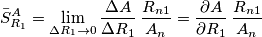
 e anche
e anche 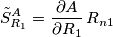
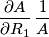 e` misurata in reciproco di ohm, mentre
e` misurata in reciproco di ohm, mentre 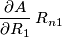 ha le unita` di misura di
ha le unita` di misura di 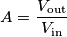 di questo circuito al variare dei parametri:
di questo circuito al variare dei parametri: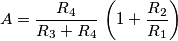 Se i componenti fossero ideali, il guadagno sarebbe 5.6 volte. Calcoliamo adesso le sensitivities relative (viene parecchia algebra), cominciando da
Se i componenti fossero ideali, il guadagno sarebbe 5.6 volte. Calcoliamo adesso le sensitivities relative (viene parecchia algebra), cominciando da 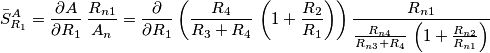
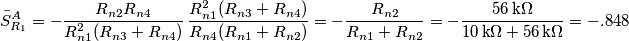
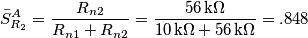
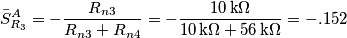
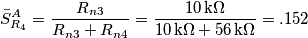

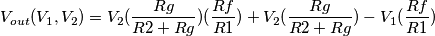
 ad ambedue le tensioni (che per comodita' penso siano uguali a 0), trovando quindi:
ad ambedue le tensioni (che per comodita' penso siano uguali a 0), trovando quindi: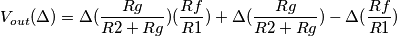
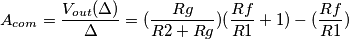
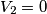 ) variando solo l' altra (per comodita'
) variando solo l' altra (per comodita'  ) e di conseguenza:
) e di conseguenza: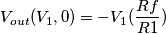
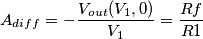
 ) perche' quel guadagno pressupporrebbe altrimenti che la tensione differenziale in ingresso sia (
) perche' quel guadagno pressupporrebbe altrimenti che la tensione differenziale in ingresso sia (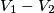 ), invece nel mio caso la tensione in ingresso e' (
), invece nel mio caso la tensione in ingresso e' (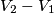 ), ovvero il potenziale maggiore "entra" nel morsetto
), ovvero il potenziale maggiore "entra" nel morsetto  dell' OP-AMP (opportunamente scalato dal partitore resistivo).
dell' OP-AMP (opportunamente scalato dal partitore resistivo).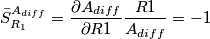
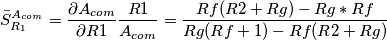
 . Essendo lineare, puo` solo essere del tipo
. Essendo lineare, puo` solo essere del tipo  Ho messo il segno negativo ad
Ho messo il segno negativo ad  cosi` dopo ci si ritrova, ma ci sono anche altre analisi senza segno meno esplicito.
cosi` dopo ci si ritrova, ma ci sono anche altre analisi senza segno meno esplicito.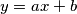
 non si da` molta informazione in piu` su come funziona bene o male l'ampli differenziale.
non si da` molta informazione in piu` su come funziona bene o male l'ampli differenziale. e
e  , ciascuna moltiplicata per la propria costante, e` molto piu` significativo mettere in evidenza l fatto che la differenza di tensione fra
, ciascuna moltiplicata per la propria costante, e` molto piu` significativo mettere in evidenza l fatto che la differenza di tensione fra  .
. perche' stiamo perdendo una dimensione: siamo partiti da due tensioni e ne abbiamo solo una: questa non e` una rappresentazione equivalente.
perche' stiamo perdendo una dimensione: siamo partiti da due tensioni e ne abbiamo solo una: questa non e` una rappresentazione equivalente.  definita in questo modo:
definita in questo modo:  . In pratica
. In pratica  mentre le altre sono
mentre le altre sono 
 otteniamo
otteniamo  e per il modo comune
e per il modo comune  . Se prendiamo queste due tensioni e le mettiamo nelle due equazioni di sinistra, riotteniamo
. Se prendiamo queste due tensioni e le mettiamo nelle due equazioni di sinistra, riotteniamo 
 dove si e` definito
dove si e` definito
 il guadagno differenziale vale
il guadagno differenziale vale  mentre quello di modo comune vale
mentre quello di modo comune vale  . In effetti l'amplificatore differenziale lo si utilizza proprio per non sentire il modo comune e amplificare invece di una quantita`
. In effetti l'amplificatore differenziale lo si utilizza proprio per non sentire il modo comune e amplificare invece di una quantita`  non siano proprio identici, e quindi avremo errori su
non siano proprio identici, e quindi avremo errori su  e su
e su  . Calcoliamo prima queste due grandezze in funzione delle resistenze e poi ci facciamo su i conti. Faccio riferimento al mio schema che ha dei nomi umani per le resistenze. I valori vedremo dopo che non sono importanti.
. Calcoliamo prima queste due grandezze in funzione delle resistenze e poi ci facciamo su i conti. Faccio riferimento al mio schema che ha dei nomi umani per le resistenze. I valori vedremo dopo che non sono importanti. e per
e per 
 e
e  (o anche solo
(o anche solo  e
e  , con
, con  una costante qualunque) si avrebbe
una costante qualunque) si avrebbe  e
e  e
e  c'e` la resistenza interna della sorgente che puo` provocare danni
c'e` la resistenza interna della sorgente che puo` provocare danni Al posto della generica
Al posto della generica 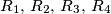
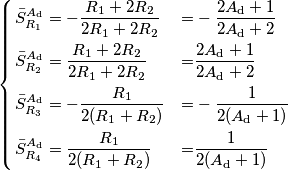
 , al solito valutata per le quattro diverse resistenze. Da osservare che anche questa sensitivity e` adimensionata. I risultati sono (con il solito pacco di algebra, sempre se non ho sbagliato i conti)
, al solito valutata per le quattro diverse resistenze. Da osservare che anche questa sensitivity e` adimensionata. I risultati sono (con il solito pacco di algebra, sempre se non ho sbagliato i conti)
 e
e  sono negativi: se
sono negativi: se  e
e  sono positive: se
sono positive: se  e
e  diminuiscono, il guadagno diminuisce.
diminuiscono, il guadagno diminuisce. 

 e questo potrebbe essere un grosso guaio.
e questo potrebbe essere un grosso guaio.  . Ci serve un guadagno differenziale
. Ci serve un guadagno differenziale  e se facciamo le cose per bene il guadagno di modo comune
e se facciamo le cose per bene il guadagno di modo comune 
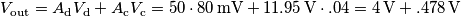
 . Nell'esempio fatto, si ha
. Nell'esempio fatto, si ha  . Gli amplificatori da strumentazione integrati arrivano oltre al centinaio di decibel.
. Gli amplificatori da strumentazione integrati arrivano oltre al centinaio di decibel.

