ElectroYou - la comunità dei professionisti del mondo elettrico

da **daniloG** » 26 gen 2010, 18:16

Salve a tutti ragazzi,
dato che volevo ottenere una tensione negativa senza l'uso di un trasformatore con zero centrale avevo pensato di usare un condensatore sollecitato da un onda quadra:

: cir1; Immagine.JPG (5.23 KiB) Osservato 15622 volte

ora io ho analizzato in questo modo:
Il primo condensatore si caricherà con costante di tempo

dove

è uguale al prodotto di

in questo caso r e la resistenza d'uscita del generatore quindi suppongo che per avere il condensatore completamente carico dovrò avere Ton > 5t

, durante il periodo di Toff ho considerato il condensatore come una piccola batteria carica di polarità invertita, quindi in questo periodo la capacità dovra fornire corrente sia al secondo condensatore sia al carico quindi Ic1 = Ic2 + Iout

, mentre durante il periodo di Ton sarà il secondo condensatore a dover fornire corrente al carico.
Se quanto ho detto non è una vaccata come procedo per calcolarmi le capacità?
ps (In questo caso il generatore d' onda quadra sarà un 555 e la massima corrente sara data da la corrente di sink dello stesso)
Grazie in anticipo

da **g.schgor** » 26 gen 2010, 19:18

Puoi dirci qual è la tensione del generatore di onda quadra,
e che tensione e corrente di uscita desideri?

da **IsidoroKZ** » 27 gen 2010, 5:39

daniloG ha scritto:Se quanto ho detto non è una vaccata come procedo per calcolarmi le capacità?

Non e` per nulla una vaccata. Il circuito pilotato con un'onda quadra (ma anche se fosse sinusoidale non cambierebbe nulla, tranne che per il ripple di uscita) passa attraverso i periodi (stati) $T_\text{on}$ e $T_\text{off}$ in cui puo` essere modellato in questo modo (i condensatori elettrolitici sono solo per mostrare le polarita` effettive,
I don't endorse either explicitely recommend using electrolytic capacitors, or neither I deem electrolytic capacitors outperform other technologies

)

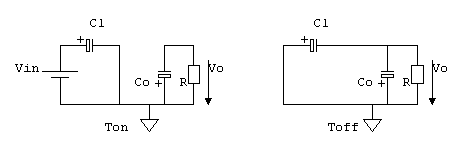
: CapComm.gif (1.5 KiB) Osservato 15497 volte

Dove ho indicato con Vin il livello alto di tensione e ho considerato il livello basso pari a 0V. Se la tensione di ingresso variasse fra Vinh e Vinl quello che segue non cambierebbe tranne nel fatto che al posto di Vin si dovrebbe usare Vinh-Vinl. Quello che conta e` solo il valore picco picco della tensione di ingresso, che vada da 0V a 12V, da -6V a +6V, da 24 V a 36V non cambia nulla: il valore continuo e` assorbito e annullato dal condensatore C1.

Ho anche trascurato la caduta sui diodi, cosa non troppo lecita se le tensioni sono basse. Piu` avanti, introdurro` anche l'effetto della caduta sui diodi $V_\text{D}$ .

Altra assunzione che si fa e` che la tensione di uscita Vo, positiva per come ho preso il verso, sia praticamente costante. In pratica si fa l'approssimazione di piccolo ripple. Non e` necessario ipotizzare di essere in condizioni stazionarie, basta supporre che la tensione media di uscita, se cambia, cambi lentamente.

La tensione che questo circuito genera ha segno opposto rispetto all'ingresso. In questa trattazione, per comodita` prendo la tensione di uscita "a rovescio" in modo da non avere troppi segni negativi per i piedi, meta` dei quali andrebbero persi

. Ripeto: la tensione di uscita di questo circuito e` negativa, la misuro solo a rovescio.

A questo punto le cose si svolgono esattamente come hai detto: durante $T_\text{on}$ la tensione sul condensatore C1 vale Vin, mentre durante Toff vale Vo

$\left\{\begin{matrix}V_\text{C}_1=V_\text{in} & \text{durante }T_\text{on} \\ V_\text{C}_1=V_\text{o} & \text{durante }T_\text{off} \end{matrix}$

La variazione di tensione su C_1

vale quindi, in ogni ciclo $\Delta V_\text{C}_1=V_\text{in}-V_\text{o}$ e la variazione di carica $\Delta Q$ sul condensatore vale
$\Delta Q=C_1\,\Delta V=C_1(V_\text{in}-V_\text{o})$

Ad ogni ciclo questa carica $\Delta Q$ viene fornita a Co e al carico. Questa operazione si ripete $f_\text{sw}=\frac{1}{T_\text{on}+T_\text{off}}$ volte per unita` di tempo e la carica fornita per unita` di tempo costituisce la corrente media fornita al carico:

$I=\Delta Q\,f_\text{sw}=C_1(V_\text{in}-V_\text{o})f_\text{sw}$

La corrente media fornita al carico e` quella che scorre attraverso R, perche' nel condensatore Co la corrente media vale 0 (come in tutti i condensatori non guasti).

Il valore di capacita` da mettere e` quindi $C_1=\frac{I_\text{o}}{f_\text{sw}(V_\text{in}-V_\text{o})}$

Da osservare un paio di particolari. La tensione di uscita $V_\text{o}$ e` comunque in modulo minore di $V_\text{in}$ se si vuole erogare una corrente $I_\text{o}$ sul carico. La relazione che fornisce la capacita` del condensatore puo` anche essere scritta come

$C_1=\frac{V_\text{o}}{f_\text{sw}R(V_\text{in}-V_\text{o})}$ .

La seconda osservazione, importate, e` che la "caduta di tensione" fra ingresso e uscita vale $V_\text{in}-V_\text{o}=\frac{I_\text{o}}{f_\text{sw}C_1}$ . In pratica questo convertitore si comporta come se fra ingresso e uscita ci fosse una resistenza equivalente di valore: $R_\text{eq}=\frac{1}{f_\text{sw}C_1}}$
Questa resistenza equivalente e` una resistenza a tutti gli effetti, scalda come tutte le resistenze (vedi questo semplice articolo di sua maesta` Renzo I DF).

Vediamo ora qualche considerazione sulla frequenza $f_\text{sw}$ : minore e` la frequenza di commutazione, piu` grande dovra` essere la capacita` $\text{C}_1$ . D'altra parte non si puo` alzare troppo la frequenza perche' bisogna lasciare il tempo alla capacita` di caricarsi durante $T_\text{on}$ e scarcarsi durante $T_\text{off}$ . In realta` credo che questa seconda richiesta non sia fondamentale, ma confesso di non avere mai indagato. Il tempo di carica e` anche determinato dalla resistenza di sorgente, mentre quello di scarica e` solo dato dalle resistenze parassite, ESR dei condensatori, diodi...

Vediamo ora l'effetto ella caduta sui diodi. L'analisi e` semplicissima: si parte dalla variazione della tensione sul condensatore $\text{C}_1$ nei due stati, considerando una caduta di tensione fissa di valore pari a $V_\text{D}$ . Lo schema equivalente e`il seguente

: capcomm2.gif (1.55 KiB) Osservato 15481 volte

Rifacendo tutta l'analisi come in precedenza si ha che le tensioni su $\text{C}_1$ valgono

$\left\{\begin{matrix}V_\text{C}_1=V_\text{in}-V_\text{D} & \text{durante }T_\text{on} \\ V_\text{C}_1=V_\text{o}+V_\text{D} & \text{durante }T_\text{off} \end{matrix}$

La variazione di tensione su C_1

vale quindi, in ogni ciclo $\Delta V_\text{C}_1=V_\text{in}-V_\text{D}-(V_\text{o}+V_\text{D})=V_\text{in}-V_\text{o}-2V_\text{D}$ e la variazione di carica $\Delta Q$ sul condensatore vale

$\Delta Q=C_1\,\Delta V=C_1(V_\text{in}-V_\text{o}-2V_\text{D})$

Rifacendo tutti i passaggi come prima, la capacita` C_1

in questo caso deve avere il valore:

$C_1=\frac{I_\text{o}}{f_\text{sw}(V_\text{in}-V_\text{o}-2V_\text{D})}=\frac{V_\text{o}}{f_\text{sw}R(V_\text{in}-V_\text{o}-2V_\text{D})}$

Prima osservazione: se vogliamo ottenere qualcosa in uscita, sara` meglio che $V_\text{in}\gg 2V_\text{D}$ . E poi bisogna ricordare che comunque c'e` sempre la caduta "resistiva" sulla resistenza equivalente $R_\text{eq}=\frac{1}{f_\text{sw}C_1}}$ .

Passiamo adesso al condensatore Co. Questo componente serve ad immagazzinare energia durante la fase si scarica di C1 e a fornire energia al carico durante tutto il resto del tempo. In pratica Co viene scelto per controllare il ripple di uscita. L'analisi che segue vale solo per onda quadra in ingresso, ed e` un worst case. Se la tensione in ingresso fosse una sinusoide, il ripple sarebbe minore.

Si puo` assumere che il condensatore C1 si scarichi molto velocemente su Co, e quindi Co deve "tenere su" il carico per un tempo pari a $T_\text{sw}=\frac{1}{f_\text{sw}}$ . In realta` questo non e` proprio corretto perche' durante la fase $T_\text{on}$ in parallelo a Co c'e` anche C1, ma se lo si trascura ci si pone in una situazione piu` critica e si trovera` alla fine un risultato reale migliore, con meno ripple, di quello calcolato.

Dato che la corrente di uscita vale $I_\text{o}=\frac{V_\text{o}}{R}$ e che questa corrente viene assorbita dal condensatore di uscita $\text{C}_\text{o}$ , il ripple picco picco di uscita Vr, cioe` la variazione di tensione sul condensatore sara` pari a

$V_\text{r}=\Delta V_\text{C}_\text{o}=\frac{\Delta Q_\text{C}_\text{o}}{C_\text{o}}=\frac{I_\text{o}T_\text{sw}}{C_\text{o}}=\frac{I_\text{o}}{f_\text{sw}C_\text{o}}=\frac{V_\text{o}}{f_\text{sw}RC_\text{o}}$

C'e` un altro modo di calcolare il ripple di uscita. La variazione di carica su Co e` uguale a quella di C1, calcolata in precedenza. L'espressione alternativa del ripple di uscita quindi diventa

$V_\text{r}=\frac{\Delta Q_\text{C}_\text{o}}{C_\text{o}}=\frac{\Delta Q}{C_\text{o}}=\frac{C_1}{C_\text{o}}(V_\text{in}-V_\text{o}-2V_\text{D})}$

L'ultima espressione ci dice che per avere un basso ripple $C_\text{o} \gg C_1$ e che quando si aumenta l'assorbimento di corrente di uscita, non solo la tensione scende, ma il ripple aumenta.

Invertendo le equazioni della tensione di ripple si ottiene il valore di Co (le tre espressioni sono equivalenti, si usa la piu` comoda:

$C_\text{o}=\frac{I_\text{o}}{f_\text{sw}V_\text{r}}=\frac{V_\text{o}}{f_\text{sw}RV_\text{r}}=C_1\frac{V_\text{in}-V_\text{o}-2V_\text{D}}{V_\text{r}}$

Questa equazione e` valida per condensatori ceramici o a film, in quanto fa uso del valore capacitivo del condensatore. Se si usano degli elettrolitici e si sale di frequenza oltre 10kHz-20kHz per gli alluminio, e oltre 50kHz-100kHz per il tantalio, il condensatore cessa di comportarsi come tale e diventa, per la frequenza di commutazione, una resistenza di valore pari alla sua ESR. I conti diventano molto piu` complicati

ESEMPIO

Vin=9V, Vo=7V (sempre presa con il verso positivo, quella "vera" e` negativa), Vd=0.7V, Io=25mA, fsw=50kHz, Vr=50mV

Si tratta di calcolare prima la capacita` C1:

$C_1=\frac{I_\text{o}}{f_\text{sw}(V_\text{in}-V_\text{o}-2V_\text{D})}=\frac{25\,\text{mA}}{50\,\text{kHz}\,(9\,\text{V}-7\,\text{V}-1.4\,\text{V})}=820\,\text{nF}$

Assumento un'onda quadra simmetrica, i periodi $T_\text{on}$ e $T_\text{off}$ in questo esempio valgono $T_\text{on}=T_\text{off}=\frac{1}{2f_\text{sw}}=10\,\mu\text{s}$ . In questo intervallo di tempo C1 deve riuscire a caricarsi e scaricarsi completamente (diciamo almeno 3 costanti di tempo). La resistenza massima che deve vedere il condensatore deve essere $R_\text{max}=\frac{T_\text{on/off}}{3 C_1}=\frac{10\,\mu\text{s}}{3\cdot 820\,\text{nF}}=4\,\Omega$

Cosa capita se questa resistenza e` maggiore? Funziona ugualmente, ma con rendimento minore. In particolare la resistenza di sorgente va in serie alla resistenza equivalente $R_\text{eq}=\frac{1}{f_\text{sw}C_1}=\frac{1}{50\,\text{kHz}\cdot 820\,\text{nF}}=24\,\Omega$ e ripartisce la tensione disponibile.

Poi si calcola la capacita` di uscita: $C_\text{o}=\frac{I_\text{o}}{f_\text{sw}V_\text{r}}=\frac{25\,\text{mA}}{50\,\text{kHz}\cdot 50\,\text{mV}}=10\,\mu\text{F}$

Da osservare che quando il fattore $\Delta V_\text{C}_1=(V_\text{in}-V_\text{o}-2V_\text{D})$ che compare in tante espressioni diventa piccolo rispetto alle altre tensioni, si e` in presenza di un progetto "tirato".

Mentre la tensione di uscita e` ragionevolmente precisa, la stima del ripple e` molto piu` scadente: per fortuna che il ripple vero e` minore di quello stimato. Tutti i parametri parassiti, tranne l'ESR del condensatore di uscita, concorrono a ridurre il ripple. In particolare la resistenza di sorgente, le resistenze dei diodi...

I risultati di una simulazione con i valori indicati sopra sono riportati in questa figura:

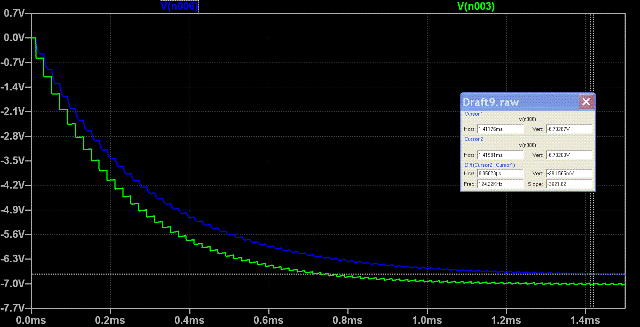
: capComm3.GIF (21.75 KiB) Osservato 15446 volte

La curva verde si riferisce a una simulazione quasi ideale: la tensione di uscita vale -7V, il ripple 41mV circa, e i picchi di corrente nei diodi sono decisamente elevati (situazione non realistica)
La curva blu invece si riferisce a un caso piu` reale: resistenza in serie a C1 di 5 ohm, tempi di salita e discesa dell'onda quadra piu` lunghi. Gli effetti sono una tensione negativa di -6.8V e il ripple di circa 28mV. La cosa piu` importante e` che la corrente nei diodi ora e` decisamente piu` bassa, dell'ordine del centinaio di milliampere.

Da notare che la curva blu ha una resistenza di uscita piu` elevata (maggiore caduta di tensione) e una costante di tempo piu` lunga per caricare il condensatore di uscita. La costante di tempo del caso ideale e` di circa 230us, mentre nel caso piu` reale siamo dalle parti di 290us.
Nel caso ideale la costante di tempo e` data dalla resistenza equivalente di 24.4 ohm in parallelo al carico di 280 ohm moltiplicato per la capacita` di uscita in parallelo a meta` di C1 (solo durante Toff C1 e` nella maglia di uscita.
$\tau=\left(\frac{1}{f_\text{sw}C_1}\parallel R\right)\left(C_\text{o}+\frac{C_1}{2}\right)=22.4\,\Omega\cdot 10.4\,\mu\text{F}=233\,\mu\text{s}$ . Close enough

da **giorgio25760** » 27 gen 2010, 7:55

Che dire Isidoro ?

Impeccabile ! (come sempre)

=D>

Ciao
Giorgio

da **brabus** » 27 gen 2010, 10:42

La cura e la passione che emergono dal tuo scritto sono degne di lode. Complimenti sinceri. =D>

da **daniloG** » 27 gen 2010, 23:59

Grazie Isidoro sei stato impeccabile,
questo va a finire direttamente negli appunti!

ps. (Che software usi per la simulazione?)

da **IsidoroKZ** » 28 gen 2010, 1:12

daniloG ha scritto:ps. (Che software usi per la simulazione?)

LTspice (e in altri casi Cadence Orcad).

Tieni presente che tutto quello che ho raccontato, mutatis mutandis, vale anche per gli altri tipi di convertitori di questo genere, e fanno tutti parte della famiglia dei circuiti a capacita` commutate, normalmente usate per i filtri, ma anche per alimentatori piccolini. Nel campo degli alimentatori al posto di capacita` commutate spesso li chiamano a pompa di carica, ma e` la stessa cosa.

Ci sono circuit integrati che fatto queste funzioni di alimentazione con efficienze abbastanza elevate. Per ottenerle, al posto di usare un'onda quadra e un circuito a diodi, usano la tensione continua dell'ingresso e interruttori comandati. Ad esempio il MAX828 e` fatto con interruttori comandati, ma sempre basato sullo stesso principio di funzionamento.

da **daniloG** » 28 gen 2010, 1:29

Perfetto,
Lo terrò presente!
Grazie di tutto.

da **trip** » 18 set 2010, 10:02

Buon giorno a tutti
sono nuovo di questo forum così come dell'elettronoca per cui se diro qualche castoneria perdonatemi.
ho qualche perplessita sul funzionamento del circuito in questione e spero che qualcuno di voi poss darmi delucidazioni in merito.
Nel semiperiodo con Vin H il condensatore si carica e il diodo collegato a massa (che per semplicita chiamero D1)conduce mentro l'altro D2 che e polarizzato inversamente risulta essere un circuito aperto.E qua nasce il primo problema: come fa l'altro condensatore C2 (quello della maglia di destra)a caricarsi se solo un terminale è collegato a massa???
Di conseguenza con Vin L il condensatore C1 si scarica, D1 e D2risultano essere un circuito aperto e D2 un corto circuito.grazie mille per chi mi dara delucidazioni in merito
ciao

da **g.schgor** » 18 set 2010, 10:24

(x trip)
Una volta che il primo condensatore (maglia sinistra) è carico
(osserva la polarità) e il generatore torna a 0, ci sono le condizioni
per caricare il secondo condensatore (maglia destra), scaricando il primo.
Sei d'accordo?

ElectroYou - la comunità dei professionisti del mondo elettrico

condensatore e tensione negativa

[1] condensatore e tensione negativa

[2] Re: condensatore e tensione negativa

[3] Re: condensatore e tensione negativa

[4] Re: condensatore e tensione negativa

[5] Re: condensatore e tensione negativa

[6] Re: condensatore e tensione negativa

[7] Re: condensatore e tensione negativa

[8] Re: condensatore e tensione negativa

[9] Re: condensatore e tensione negativa

[10] Re: condensatore e tensione negativa

Chi c’è in linea

Informazioni

Seguici

Pubblicità

Credits