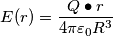Girovagando per la rete in cerca di una soluzione alle mie difficoltà mi sono imbattuto in questo topic, trovando fortunatamente qualcuno che ha avuto il mio stesso problema.
Studiando dal mio libro di Fisica II ho trovato un esempio, non spiegato in modo chiarissimo, di questa tipologia di esercizio.
Tale esempio spiega come calcolare il campo elettrico nel caso di una distribuzione sferica con cavità sferica interna non concentrica, quindi simile a quello della traccia. Nel mio caso, non vengono dati numeri, ma solo delle formule, senza tutto il ragionamento matematico che bisogna seguire per ottenerle. Tuttavia sul libro ho trovato scritto, come suggerito anche da RenzoDF, di utilizzare il teorema di
gauss associato al principio di sovrapposizione per ottenere il campo E come somma di contributi generati da distribuzioni di carica perfettamente simmetriche.
Secondo quanto riportato sul testo dovrei considerare la sfera carica con cavità sferica vuota come equivalente ad una sfera piena(senza cavità) di raggio R1 (nel nostro caso 5 cm), con centro O e densità di carica rho1 (ϱ1), più una seconda sfera di raggio R2(nel nostro caso 2 cm), centro O' e densità di carica rho2 ( ϱ2).
Ho provato a risolvere l'esercizio con i dati forniti in traccia e con le uniche formule date dal testo (che non spiega come arrivarci):

con

Provando ad applicare le formule con i dati forniti dal problema ho ottenuto il valore di 0,95 (nella formula del campo elettrico ho ottenuto il valore di OP utilizzando il teorema di pitagora, ottenendo quindi il valore 2,24).
Non riuscendo a capire da dove venissero quelle formule, ho provato a fare come spiegato sul testo, cioè a calcolare i campi elettrici delle due sfere e sommarli algebricamente.
Ho quindi ottenuto applicando le formule generali del campo elettrico in una distribuzione spaziale sferica:

e

Dalla prima ho ottenuto

e dalla seconda, grazie al suggerimento dato da RenzoDF a riguardo della carica

ho ottenuto il valore

quindi, sommando le due ho ottenuto

quindi se i calcoli sono corretti, dovrei ritrovarmi con il libro di testo.
Tuttavia, pur essendo riuscito a risolvere il problema, mi è rimasto il dubbio sull'aiuto fornito da RenzoDF, cioè:
RenzoDF ha scritto:
1) Sapendo che i valori dei raggi sono 5 cm e 2 cm, elevando al cubo non dovremmo ottenere 8 e 125? Suppongo sia comunque una distrazione e che intendesse quei valori.
2) Sareste in grado di spiegarmi il ragionamento matematico da seguire per ottenere tale formula (cioè quella che mette in relazione Q2 a Q1)? Non sono riuscito a capirlo da solo, e nemmeno il libro di testo mi ha aiutato a riguardo.
3) Il procedimento seguito da me è corretto? Oppure è una coincidenza che i risultati sono gli stessi applicando la formula del libro di testo e la formula ottenuta dai miei ragionamenti?
In attesa di chiarezza riguardo alle mie questioni, vi saluto, mi congratulo per il forum (potrei diventare un membro molto assiduo visto le mie difficoltà in queste materie), e vi ringrazio anticipatamente.
- Wasp1311

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)
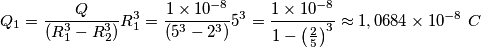
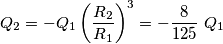













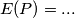 è una relazione vettoriale NON scalare
è una relazione vettoriale NON scalare  (\bullet) che hai inserito nelle tue formule serve a volte per indicare il
(\bullet) che hai inserito nelle tue formule serve a volte per indicare il 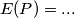 )
)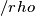 la densità spaziale di carica, pari a:
la densità spaziale di carica, pari a: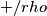 e
e 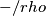 rispettivamente.
rispettivamente.