campo magnetico

[wackos]

ciao a tutti...
avrei bisogno di un'informazione:
il campo elettrico può essere rappresentato da superfici equipotenziali... mi chiedevo... per il campo magnetico vale la stessa cosa??

[admin]

Si rappresentano in generale con le linee di forza, cioè con le linee parallele in ogni punto all'induzione magnetica. Non esiste, come nel campo elettrico, una funzione scalare detta potenziale il cui gradiente corrisponde al campo elettrico. Esiste il potenziale magnetico, che però è una grandezza vettoriale più complessa.
Questa, ad esempio è la rappresentazione del campo di un magnete permanente.

lineediforza.jpg (66.48 KiB) Osservato 6553 volte

La figura è realizzata con FEMM
La lunghezza delle frecce è proporzionale all'induzione

[wackos]

scusa ma non ho capito molto bene perché non si può rappresentare attraverso superfici equipotenziali...

[admin]

Perché non si può rappresentare ciò che non esiste.
O meglio si possono rappresentare anche cose che non esistono, ma che esistono nella fantasia. Ma non siamo in questo caso.
Il potenziale elettrico è una funzione scalare che consente di calcolare l'integrale di linea del capo elettrico tra due punti semplicemente facendo la differenza tra i valori che tale funzione assume agli estremi della linea, indipendentemente dal percorso della linea che unisce i due punti. Le superfici equipotenziali del campo elettrico sono l'insieme di tutti i punti in cui la funzione ha lo stesso valore.
Nel campo magnetico tale funzione non esiste.

[DirtyDeeds]

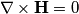In realtà, si può definire un potenziale scalare anche per il campo magnetico, nelle regioni di spazio in cui , e alcuni problemi di magnetostatica si risolvono proprio facendo così (v. qui): il problema, però, è che questo potenziale non è unico per tutto lo spazio.

[admin]

Si, hai ragione DirtyDeeds. Ho scritto una sciocchezza. Non sono orgoglioso di averla scritta, anzi, ma la metto in evidenza perché c'è chi sta girando nel forum sostenendo che se un "graduato", diciamo così, la dice quello di "grado inferiore" deve dire che ha comunque ragione.
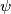Nelle regioni in cui il rotore del campo è nullo, quindi dove non ci sono correnti, si può definire una funzione scalare , come quella del potenziale elettrostatico, da cui derivare il campo magnetico come gradiente cambiato di segno. Io ho pensato solo al caso generale, che comprende tutto lo spazio. Hai fatto bene ad evidenziare che esiste la possibilità di procedere in modo identico. Quindi ho sbagliato a dire che è una grandezza inesistente. Vi sono stato indotto anche dal fatto che FEMM ,ad esempio, nella rappresentazione del campo magnetico, dà la possibilità di farlo con le linee di forza e non propone superfici equipotenziali da tracciare nelle regioni in cui sarebbe possibile. Ma ovviamente questo non giustifica un'affermazione di impossibilità o di inesistenza come la mia.

[DirtyDeeds]

C'è però un'altra differenza fondamentale tra il potenziale elettrico e il potenziale scalare magnetico, che rende quest'ultimo meno interessante del primo (e che rende anche poco utile il tracciare le superfici equipotenziali). Il potenziale elettrico (e anche quello gravitazionale) ha una duplice utilità:

1) permette di ridurre problemi vettoriali a problemi scalari, più facilmente risolvibili;
2) permette di determinare il lavoro necessario per spostare una carica (o una massa, nel caso di quello gravitazionale) attraverso il campo.

Il potenziale scalare magnetico, invece, non è legato al concetto di lavoro e per esso, quindi, vale solo il primo punto.

[wackos]

quindi alla fine posso rappresentarlo tramite superfici equipotenziali??
in ogni caso mi riuscite a spiegare in modo semplice il perché... grazie mille in anticipo ... ciao ciao

[DirtyDeeds]

La risposta semplice è: non usare quella rappresentazione, soprattutto se non sei riuscito a seguire ciò che è stato scritto sopra, potresti fare grossi errori. Prima dicci qual è il tuo livello di fisica/matematica e cosa stai studiando, così riusciamo a dosare meglio la risposta. E soprattutto: perché vorresti rappresentare il campo magnetico in quel modo?

[wackos]

no non è che voglio rappresentarlo...era solo per capire dato che ho sentito gente all'università che ne parlava ma non ci ho capito niente... comunque sto facendo ingegneria..