ElectroYou - la comunità dei professionisti del mondo elettrico

da **PietroBaima** » 17 set 2012, 20:36

Ciao a tutti.
Da un po' di tempo mi sto trastullando a studiare gli oscillatori autonomi quasi sinusoidali, prima su un newsgroup di fisica e adesso qui.
Volevo proporvi le mie riflessioni, evinte dopo averne discusso nel newsgroup (grazie a tutti coloro che mi hanno elargito i loro preziosi consigli!) e avere i vostri preziosissimi suggerimenti e consigli o, anche meglio, le vostre preziosissime correzioni. Ditemi che cosa ne pensate, e, più in generale, tutto quel che volete; starà a me trarne qualcosa di utile. Se vi va, naturalmente! Grazie a tutti!! Ciao da Pietro. O_/

_____________________________________________________________________________________________
Condizioni di oscillazione

Un oscillatore autonomo quasi sinusoidale sarà sempre scomponibile in due parti, la prima delle quali composta da un amplificatore ideale e la seconda composta da una rete lineare, che risulterà conveniente esprimere tramite una matrice T, come si vedrà in seguito. Se l'amplificatore non è ideale i suoi parametri sono comunque inseribili all'interno della matrice T, che probabilmente diventerà risolubile con l'aiuto del calcolatore. In figura è riportato lo schema corrispondente.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

dove:
$\textbf{Tosc}=\left(\begin{array}{cc}\mathrm{A_{osc}} & \mathrm{B_{osc}}\\\mathrm{C_{osc}} & \mathrm{D_{osc}}\end{array}\right)$

$\left(\begin{array}{c}\mathrm{V_{1}}\\\mathrm{I_{1}}\end{array}\right)= \mathbf{T}_{\mathbf{osc}}\left(\begin{array}{c}\mathrm{V_{2}}\\\mathrm{I_{2}}\end{array}\right)$ .

Ricordo che le dimensioni fisiche delle componenti di T sono:

$\mathrm{\left[A_{osc}\right]}\mathrm{=1}$
$\mathrm{\left[B_{osc}\right]=\Omega}$
$\mathrm{\left[C_{osc}\right]=\mathrm{S}}$
$\mathrm{\left[D_{osc}\right]}\mathrm{=1}$

Avendo considerato l'amplificatore ideale si può scrivere
$\begin{cases}\mathrm{I_{2}}=0\\\mathrm{V_{1}}=\mathrm{A_{v}}*\mathrm{V_{2}}\end{cases}$
Unendo queste relazioni a quelle ricavabili dalla prima riga della matrice T si ha che:
$\mathrm{A_{v}*\mathrm{V_{2}=\mathrm{A_{osc}*\mathrm{V_{2}}}}}$
Le cui soluzioni possibili sono:

I. $\mathrm{V_{2}=0}$
$\vee$
II. $\mathrm{A_{osc}=A_{v}}$

La soluzione I. rende nulla la tensione $V_{2}$ e, per quanto possa non essere interessante, rivela che un qualunque oscillatore ha un punto di equilibrio a tensione nulla.
La soluzione II. rende indefinita la tensione $V_{2}$ e restituisce informazioni circa la frequenza di oscillazione ed il guadagno dell'amplificatore che devono essere soddisfatti per garantire le condizioni di innesco.
poiché la rete lineare contenuta nel blocco T è anche reattiva si ha che $A_{osc}\mathbb{\in C}$ , mentre $A_{v}\mathbb{\in R}$ .
Dovrà pertanto essere soddisfatto il sistema:
$\begin{cases}\Re\left(\mathrm{A_{osc}}\right)=\mathrm{A_{v}}\\\Im\left(\mathrm{A_{osc}}\right)=0\end{cases}$
La prima relazione permetterà di calcolare l'amplificazione $A_{v}$ .
La seconda relazione, essendo pari alla parte immaginaria di $A_{osc}$ e quindi dipendente da $\omega$ permetterà di ricavare la frequenza di oscillazione.
Ora si può ricordare che
$\mathrm{A_{osc}=}\left.\frac{\mathrm{V_{1}}}{\mathrm{V}_{2}}\right|_{\mathrm{I_{2}=0}}$
In conclusione, è possibile considerare la sola rete lineare contenuta nella matrice T e risovere il sistema
$\begin{cases}\Re\left(\mathrm{\frac{\mathrm{V_{1}}}{\mathrm{V_{2}}}}\right)=\mathrm{A_{v}}\\ \Im\left(\mathrm{\frac{\mathrm{V_{1}}}{\mathrm{V_{2}}}}\right)=0\end{cases}$

Esempio1. Oscillatore a ponte di Wien

Schema:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Rete equivalente divisa tra amplificatore e matrice T

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

E' necessario ricavare $\frac{\mathrm{V_{1}}}{\mathrm{V}_{2}}$ dalla rete epurata dell'amplificatore.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

E' sufficiente applicare la formula del partitore di tensione:
$\mathrm{A_{osc}=}\frac{\mathrm{V_{1}}}{\mathrm{V}_{2}}\mathrm{=1+\frac{Z_{1}}{Z_{2}}=1+\jmath\left(R-\jmath\frac{1}{\omega C}\right)^{2}\frac{\omega C}{R}=3+\jmath\left(\omega RC-\frac{1}{\omega RC}\right)}$

[Dove mi sono conformato all'uso della j in luogo della i per indicare il versore complesso in auge tra gli elettronici, di cui non faccio parte

]

Per cui la parte reale di $\mathrm{A_{osc}}$ è pari a 3 e questo è anche il guadagno che dovrà avere $\mathrm{A_{v}}$ per poter fare oscillare la rete.
La parte immaginaria, posta uguale a zero, permette di calcolare $\omega=\frac{1}{\mathrm{RC}}$ .

Esempio2. Oscillatore a sfasamento

Schema

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Ricordo che, per come ho congegnato le cose, $\mathrm{V_{1}}$ va sempre apposta all'uscita dell'amplificatore.

Se non fosse per le proprietà delle matrici T, il rapporto $\mathrm{\frac{\mathrm{V_{1}}}{\mathrm{V}_{2}}}$ sarebbe molto lungo da calcolare.
[Una cosa che proprio non mi piace fare è proprio scrivere paginate di conti per arrivare alla soluzione *sbagliata*...

]
In questa rete possiamo notare che sono collegate in cascata tre matrici T identiche, pari a:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Le matrici T collegate in cascata si moltiplicano tra loro, per cui sarà sufficiente calcolare $\mathrm{\mathbf{T}^{3}}$ , o, meglio, per come si esegue il prodotto riga-colonna, sarà sufficiente calcolare il vettore (A,B) di $\mathrm{\mathbf{T}^{2}}$ e farne il prodotto scalare con il vettore (A,C) di T.
Calcoliamo dunque la matrice T del gruppo CR.

$\mathrm{\mathbf{T}=}\mathrm{\left(\begin{array}{cc}\left.\frac{V_{1}}{V_{2}}\right|_{I_{2}=0} & \left.\frac{V_{1}}{I_{2}}\right|_{V_{2}=0}\\\left.\frac{I_{1}}{V_{2}}\right|_{I_{2}=0} & \left.\frac{I_{1}}{I_{2}}\right|_{V_{2}=0}\end{array}\right)}=\left(\begin{array}{cc}1-\jmath\frac{1}{\omega\mathrm{RC}} & -\jmath\frac{1}{\omega\mathrm{C}}\\\frac{1}{\mathrm{R}} & 1\end{array}\right)=\left(\begin{array}{cc}1-\jmath\alpha & \jmath\beta\\-\frac{\alpha}{\beta} & 1\end{array}\right)$
dove ho posto, per comodità, $\alpha=\frac{1}{\omega\mathrm{RC}}$ e $\beta=-\frac{1}{\omega\mathrm{C}}$ .

$\mathrm{\mathbf{T}^{2}=\left(\begin{array}{cc}1-\alpha^{2}-\jmath3\alpha & \alpha\beta+\jmath2\beta\\ \boxtimes & \boxtimes\end{array}\right)}$

Dove il simbolo $\boxtimes$ indica che quel valore non è necessario per calcolare $\mathrm{A_{osc}}$ di $\mathrm{\mathbf{T}^{3}}$ .
Eseguendo l'ultimo prodotto si ha che:
$\mathrm{A_{osc}=-5\alpha^{2}+1+\jmath\left(-6\alpha+\alpha^{3}\right)}$
da cui:
1. Parte immaginaria uguale a zero per trovare la $\omega$ :
$\mathrm{-6\alpha+\alpha^{3}=0}\Rightarrow\alpha=0\vee\alpha=\pm\sqrt{6}$
$\alpha=0$ e $\alpha=-\sqrt{6}$ non sono molto utili, mentre $\alpha=\frac{1}{\omega\mathrm{RC}}=\sqrt{6}\Rightarrow\omega=\frac{1}{\sqrt{6}\mathrm{RC}}$ lo è.
2. Parte reale uguale ad $A_{v}$ per trovare il guadagno:
$-5\alpha^{2}+1=\mathrm{A_{v}}$
con $\alpha=\sqrt{6}$ risulta essere $A_{v}=-29$

Sebbene questi calcoli appaiano più lunghi di quanto in realtà lo siano, capisco che la domanda: " :shock:

E' possibile fare questi calcoli in modo automatico?" sorga spontanea.
La risposta è sì, tuttavia bisogna trovare un modo per estrarre $A_{osc}$ dalla matrice T. Per farlo si potrebbe pensare di utilizzare la base canonica di $\mathbb{C}^{2}$ [La matrice T è complessa, anche se, in questo caso, non si considera $\mathbb{C}$ come $\mathbb{R}$ spazio vettoriale, quindi, in soldoni la base reale e quella complessa sono identiche].
Nel caso generale bisogna quindi calcolare:
$\Re\left(\mathrm{\vec{\mathbf{e}_{1}}\mathbf{T_{osc}}}\vec{\mathbf{e}_{1}}^{T}\right) \mathrm{=A_{v}}$
$\Im\left(\mathrm{\vec{\mathbf{e}_{1}}\mathbf{T_{osc}}}\vec{\mathbf{e}_{1}}^{T}\right) \mathrm{=0}$
[la T ad apice indica l'operatore "trasposto di"]
Queste sono formule generali, che vanno bene per risolvere un oscillatore qualunque, di cui si conosca la sua matrice T.
Nel caso dell'oscillatore in corso di sevizie si ha che $\mathrm{\mathbf{T}_{osc}=\mathrm{\mathbf{T}^{3}}}$ , quindi:
$\Re\left(\mathrm{\vec{\mathbf{e}_{1}}\mathbf{T^{3}}}\vec{\mathbf{e}_{1}}^{T}\right) \mathrm{=A_{v}}$
$\Im\left(\mathrm{\vec{\mathbf{e}_{1}}\mathbf{T^{3}}}\vec{\mathbf{e}_{1}}^{T}\right) \mathrm{=0}$

Non resta quindi che fornire ad un programma di manipolazione algebrica la formula trovata.
Quando non ho a disposizione Mathematica sul calcolatore che uso, in genere uso WolframAlpha, dal sito http://www.wolframalpha.com.
Si può provare a digitare il comando:

Codice: Seleziona tutto: Solve[Im[{1, 0}.MatrixPower[{{1-I*Re[a], I*b}, {-Re[a]/b, 1}}, 3].{{1}, {0}}] == 0, a]

per ottenere le soluzioni in $\alpha$ di questo oscillatore.
Dopo aver quindi ottenuto, come soluzione, $\alpha=\sqrt{6}$ , con il comando

Codice: Seleziona tutto: Solve[Re[{1, 0}.MatrixPower[{{1-I*Sqrt[6], I*b}, {-Sqrt[6]/b, 1}}, 3].{{1}, {0}}] == A, A]

Si otterrà il relativo guadagno $A_{v}$ .
Chi ha letto il comando avrà notato che ho inserito Re[a] e non a, la ragione è che spesso WolframAlpha ipotizza le costanti come complesse.
Non è necessario, invece, preoccuparsi troppo per la costante b inserita nella formula, poiché $\left[\beta\right]=\Omega$ mentre $\left[A_{osc}\right]=1$ , da cui si evince che, non essendoci altri termini di dimensione inversa nella formula, questa dovrà necessariamente semplificarsi con se stessa per renderla dimensionalmente coerente.
Qualora le tre matrici T fossero diverse tra loro (quindi qualora i componenti avessero valori tra loro diversi) bisognerebbe effettuare separatamente i prodotti delle tre matrici [esclusivo per algebristi amanti dell'estremo, usate WolframAlpha o simili :!:

] I calcoli si allungheranno molto, tuttavia il procedimento rimarrà invariato.
Se il blocco di matrice T fosse unico, esso non potrebbe dar luogo ad alcuna oscillazione, infatti si è ricavato che il termine A della matrice T è pari a $1-\jmath\alpha$ , da cui $\alpha=0$ .
Se il blocco di matrice T fosse doppio, esso, comunque, non potrebbe dar luogo ad alcuna oscillazione, infatti si è ricavato che il termine A della matrice $T^{2}$ è pari a $1-\alpha^{2}-\jmath3\alpha$ , da cui $\alpha=0$ .
E se i blocchi fossero più di tre?
4 blocchi:
Formula per trovare $\alpha$ :

Codice: Seleziona tutto: Solve[Im[{1, 0}.MatrixPower[{{1-I*Re[a], I*b}, {-Re[a]/b, 1}}, 4].{{1}, {0}}] == 0, a]

5 blocchi:
Formula per trovare $\alpha$ :

Codice: Seleziona tutto: Solve[Im[{1, 0}.MatrixPower[{{1-I*Re[a], I*b}, {-Re[a]/b, 1}}, 5].{{1}, {0}}] == 0, a]

e così via.
Un punto interessante che ho trovato alzando il grado della matrice T è che se i blocchi fossero cinque avremmo due soluzioni valide per $\alpha$ , scartando $\alpha=0$ .
Quindi la rete oscillerebbe a due frequenze diverse cambiando il guadagno dell'amplificatore.
Tuttavia, salendo di grado anche oltre il quinto, alcune delle soluzioni trovate non saranno realizzabili perché il guadagno $A_{v}$ sarà troppo alto per poter essere realizzato.
Con un numero di blocchi pari ad $\mathrm{n\in\mathbb{N}}$ è facile dimostrare che il numero delle soluzioni valide sia $\mathrm{s=\left\lfloor \frac{n-1}{2}\right\rfloor }$ .
La ragione è dovuta al fatto che la soluzione $\alpha=0$ dovrà essere sempre presente, perché un oscillatore, come già detto all'inizio, dovrà sempre avere un punto stabile nullo, inoltre se è presente una soluzione dovrà essere presente anche la sua complessa coniugata (la funzione che si analizza è hermitiana). Dovendo scartare le soluzioni negative è quindi più chiara la ragione per la quale un solo blocco o un blocco doppio non possano oscillare, mentre il blocco di grado tre abbia una sola soluzione valida.
Mi sono anche avventurato nel trovare una formula generale per il caso n-esimo. Ci sono riuscito, ma non credo di aver trovato nulla di utile.Tuttavia il fatto che io non abbia trovato nulla di utile potrebbe non voler dire nulla. Lo schema per arrivarci, senza dilungarmi troppo, è che non conviene diagonalizzare T secondo lo schema canonico $\mathrm{\mathbf{T}^{n}=\mathbf{P}\mathbf{T}_{diag}\mathbf{P}^{-1}}$ perché il procedimento diventa intrattabile in termini di calcoli [provate con WolframAlpha.Andrà in timeout...]

Codice: Seleziona tutto: Solve[Im[{1, 0}.MatrixPower[{{1-I*Re[a], I*b}, {-Re[a]/b, 1}}, n].{{1}, {0}}] == 0, a]

Conviene invece approssimare con Chebychev, ricordando che $\cos\left(\mathrm{n}*\arctan\left(x\right)\right)\mathrm{=C_{n}^{-1}\left(\frac{1}{1+x^{2}}\right)}$ dove $C_{n}^{-1}$ è il polinomio approssimante n-esimo inverso di Chebychev. Ma forse conviene lasciar perdere.
La conclusione è che facendo crescere n il sistema acquisisce gradi di libertà e di conseguenza anche "modi" per poter oscillare (e la cosa comincia a ricordarmi, per certi versi, le linee di trasmissione).

Esempio3. Oscillatore a R negativa

Schema

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Il gruppo $A_{v}$ ,R forma un NIC.
Applicando il partitore di tensione per le ammettenze:
$\mathrm{\frac{V_{1}}{V_{2}}=1+\frac{Y_{2}}{Y_{1}}=\left(1+\frac{R}{R_{L}}\right)+\jmath\left(\omega RC-\frac{R}{\omega L}\right)}$
Quindi:
$\mathrm{A_{v}=1+\frac{R}{R_{L}}}$
poiché la resistenza equivalente simulata dal NIC è pari a:
$\mathrm{R_{eq}=\frac{R_{NIC}}{1-A_{NIC}}}$ si ha che $\mathrm{R_{eq}=\frac{R}{1-A_{v}}=-R_{L}}$
cioè il NIC deve compensare perfettamente la resistenza di perdita dell'induttore (nell'ipotesi di trascurare quella del condensatore, che non sposta molto la trattazione).
Infine
$\omega\mathrm{RC=\frac{R}{\omega L}}\Rightarrow\omega=\frac{1}{\sqrt{\mathrm{LC}}}=\frac{1}{\mathrm{\sqrt{\frac{L}{C}}C}}=\frac{1}{\mathrm{R_{LC}C}}$

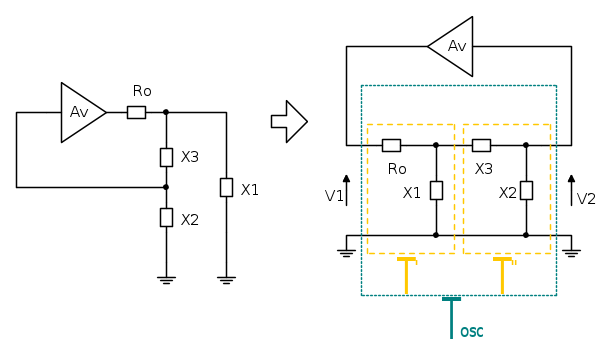
Esempio4. Oscillatore a tre punti

Schema

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Questo circuito richiede di dover considerare la resistenza Ro di uscita dell'amplificatore, altrimenti la reattanza X1 non potrà essere considerata, in quanto posta in parallelo all'uscita di un amplificatore ideale.
Il circuito è divisibile nelle matrici T' e T". L'obiettivo dell'analisi della rete è trovare il coefficiente A della matrice prodotto, pari a A'A"+B'C".
E' sufficiente trovare A' e B' dalla prima matrice:
$\mathrm{A}^{\cdot}=\left.\frac{\mathrm{V_{1}^{\cdot}}}{\mathrm{V_{2}^{\cdot}}}\right|_{\mathrm{I_{2}^{\cdot}=0}}=1-\jmath\frac{\mathrm{R_{o}}}{\mathrm{X_{1}}}$
$\mathrm{B^{\cdot}} =\left.\frac{\mathrm{V_{1}^{\cdot}}}{\mathrm{I_{2}^{\cdot}}}\right|_{\mathrm{V_{2}^{\cdot}=0}}=\mathrm{R_{o}}$

e A" e C" dalla seconda:

$\mathrm{A^{"}} =\left.\frac{\mathrm{V_{1}^{"}}}{\mathrm{V_{2}^{"}}}\right|_{\mathrm{I_{2}^{"}=0}}=1+\frac{\mathrm{X_{3}}}{\mathrm{X_{2}}}$
$\mathrm{C^{"}} =\left.\frac{\mathrm{I_{1}^{"}}}{\mathrm{V_{2}^{"}}}\right|_{\mathrm{I_{2}^{"}=0}}=-\jmath\frac{1}{\mathrm{X_{2}}}$

per poter scrivere
$\mathrm{A^{\cdot}}\mathrm{A^{"}}+\mathrm{B^{\cdot}}\mathrm{C^{"}}=\left(1-\jmath\frac{\mathrm{R_{o}}}{\mathrm{X_{1}}}\right)\left(1+\frac{\mathrm{X_{3}}}{\mathrm{X_{2}}}\right)-\jmath\frac{\mathrm{R_{o}}}{\mathrm{X_{2}}}$
Ponendo quindi la parte immaginaria pari a zero e quella reale pari al guadagno dell'amplificatore si ha che:
$\mathrm{X_{1}+X_{2}+X_{3}=0}$
poiché le varie reattanze sono composte da condensatori ed induttori (e non è possibile verificare la condizione trovata qualora il circuito sia composto esclusivamente da induttori o da condensatori) si ha che:
$\omega=\frac{1}{\sqrt{\mathrm{L_{eq}C_{eq}}}}=\frac{1}{\mathrm{\sqrt{\frac{L_{eq}}{C_{eq}}}C_{eq}}}=\frac{1}{\mathrm{R_{LC_{eq}}C_{eq}}}$
Infine:
$\mathrm{A_{v}=1+\frac{X_{3}}{X_{2}}}$
Curioso è il fatto che Ro serva ma non compaia nelle formule finali (catalizzatore? :-)

).

Esempio5. Oscillatore a T

Schema

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Lo schema è divisibile in due, "raddoppiando" $V_{1}$ . La soluzione verrà ricavata applicando il principio di sovrapposizione degli effetti.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

$V_{2}^{\cdot}$ è un risultato noto, in quanto equivale al coefficiente A di $\mathrm{\mathbf{T}^{2}}$ dell'oscillatore a sfasamento $\left[\frac{\mathrm{V_{1}^{\cdot}}}{\mathrm{V_{2}^{\cdot}}}=1-\jmath3\alpha-\alpha^{2}\right]$ .
Per $V_{2}^{"}$ invece si può usare il risultato dell'oscillatore a ponte di Wien e applicare il partitore, poiché l'uscita viene presa tra il gruppo RC serie e non sul gruppo RC parallelo.
In definitiva si ottiene:
$-\omega\mathrm{RC}\left(\left(\omega\mathrm{RC}\right)^{2}-1\right)=0\Rightarrow\omega=\frac{1}{\mathrm{RC}}$
e $A_{v}=\frac{3}{2}$

Esempio6. Oscillatore in quadratura

Schema

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Questo oscillatore è costruito collegando ad anello un integratore invertente e un integratore non invertente. Solitamente lo schema non ha l'amplificatore che ho disegnato in rosso.
Esso è stato da me artificialmente inserito per poter esprimere la rete sottostante con la matrice T. Se non dovesse successivamente essere utile si potrà porre $A_{v}=1$ .
Naturalmente $\mathrm{\frac{V_{2}}{V_{1}}=-\jmath\frac{1}{\omega RC}*\jmath\frac{1}{\omega RC}}$ , da cui $A_{osc}=\left(\omega RC\right)^{2}$ .
L'unica condizione ricavabile qui è $\omega=\frac{\sqrt{\mathrm{A_{v}}}}{\mathrm{RC}}$ .
L'oscillatore oscilla tollerando un guadagno qualunque (o quasi).
Ponendo $A_{v}=1$ si ottiene la soluzione classica, altrimenti la frequenza di oscillazione dipende dalla radice quadrata del guadagno dell'amplificatore. Curioso (e utile), no?

Conclusioni:

Ogni oscillatore fin qui analizzato ha presentato una frequenza di oscillazione proporzionale a $\omega=\frac{1}{\mathrm{kR_{eq}C_{eq}}}$ con $\mathrm{k\in\mathbb{R}}$ .
Una rete unicamente induttiva o unicamente capacitiva non potrà oscillare, a meno di non simulare un componente induttivo o capacitivo con l'ausilio di un amplificatore. La formula esplicita un condensatore equivalente, presente nella rete, sia esso reale o simulato.
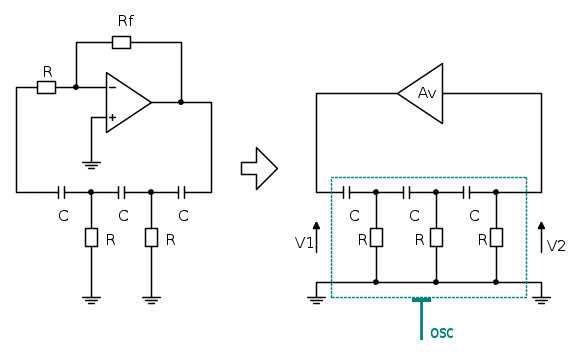
La situazione più generale potrà, quindi, essere questa:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Oppure una situazione analoga con una capacità in parallelo.
In questo schema si può osservare che è possibile far "scavalcare" alla matrice $T_{2}$ l'amplificatore $A_{v}$ e riportarla a gli ingressi di $T_{1}$ . Successivamente esse saranno due matrici T in cascata, quindi sarà possibile estrarne una matrice T equivalente, facendone il prodotto.
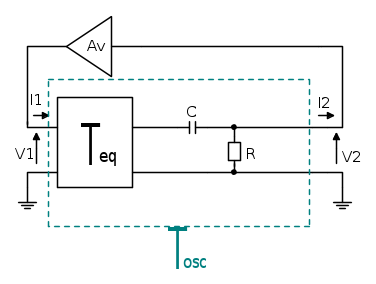
Bisognerà, tuttavia, avere l'accortezza di lasciare fuori dalla matrice $T_{2}$ una resistenza R, poiché l'amplificatore è supposto ideale.
Il circuito diventa quindi questo:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

L'obiettivo è quindi quello di capire quale sia l'impedenza vista dal condensatore, per capire il funzionamento generale di un qualsiasi oscillatore.
Si provvede quindi a estrarre il condensatore dalla rete e a sostituirlo con un generatore di corrente di test. L'impedenza equivalente sarà calcolabile facendo il rapporto tra tensione di test e corrente di test.
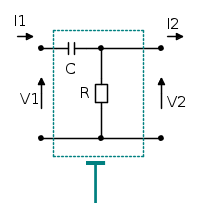
Considero quindi il circuito:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

dal quale ricavo il sistema:
$\begin{cases}\mathrm{V_{2}+V_{T}-RI_{T}=0}\\\mathrm{A_{v}RI_{T}=A_{eq}V_{2}+B_{eq}I_{T}}\end{cases}$
Dove la prima equazione è ricavabile dalla maglia posta all'uscita della matrice T, mentre la seconda è la relazione costitutiva della matrice T, considerando che $\mathrm{V_{1}=A_{v}RI_{T}}$ .
Si ricava quindi che:
$\mathrm{Z_{eq}=\frac{V_{T}}{I_{T}}=\frac{\left(A_{eq}-A_{v}\right)R+B_{eq}}{A_{eq}}}$
E' quindi necessario ricavare i coefficienti A e B della matrice T equivalente.
Per ricavarli giova osservare che il prodotto tra la matrice equivalente e la matrice T del gruppo CR dovrà essere pari alla matrice $T_{osc}$ .
$\mathrm{\mathbf{T}_{osc}=\mathbf{T}_{eq}*\mathbf{T}_{CR}}\Rightarrow\mathrm{\mathbf{T}_{eq}=\mathbf{T}_{osc}*\mathbf{T}_{CR}^{-1}}$
La matrice T del gruppo CR è sempre invertibile, poiché, essendo la rete reciproca, il suo determinante sarà pari ad uno.
La matrice del gruppo CR è stata calcolata durante la trattazione dell'oscillatore a sfasamento, ed è pari a:
$\mathrm{\mathbf{T_{CR}=}\left(\begin{array}{cc}1-\jmath\alpha & \jmath\beta\\-\frac{\alpha}{\beta} & 1 \end{array}\right)}$ , dove $\alpha=\frac{1}{\omega\mathrm{RC}}$ e $\beta=-\frac{1}{\omega\mathrm{C}}$
L'inversa di una matrice 2x2 è calcolabile ricordando la formula:
$\mathrm{\mathbf{A}^{-1}=\frac{1}{\left|\mathbf{A}\right|}\left(\begin{array}{cc}a_{22} & -a_{12}\\-a_{21} & a_{11}\end{array}\right)}$
In definitiva si ottiene:
$\mathrm{\mathbf{T_{eq}}=\left(\begin{array}{cc}A_{osc} & B_{osc}\\C_{osc} & D_{osc}\end{array}\right)\left(\begin{array}{cc}1 & -\jmath\beta\\\frac{\alpha}{\beta} & 1-\jmath\alpha\end{array}\right)}=\left(\begin{array}{cc}\mathrm{A_{osc}+B_{osc}\frac{\alpha}{\beta}} & \mathrm{B_{osc}-\jmath\left(\alpha B_{osc}+\beta A_{osc}\right)}\\\boxtimes & \boxtimes\end{array}\right)$$ .
Sostituendo le relazioni trovate nella formula di $Z_{eq}$ si ottiene:
$\mathrm{Z_{eq}=\frac{\left(A_{osc}-A_{v}\right)R}{A_{osc}-\frac{B_{osc}}{R}}}+\jmath\frac{1}{\omega\mathrm{C}}$ .

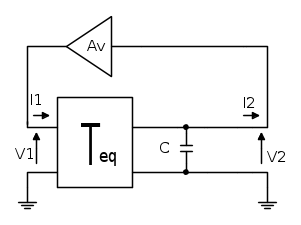
Per effettuare le considerazioni finali, è necessario studiare ancora il caso in cui il condensatore sia stato posto in parallelo, secondo questo schema:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Come per il caso precedente, la matrice $T_{2}$ si unisce alla matrice $T_{1}$ e se ne ricava una matrice equivalente.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Per calcolare, quindi $Z_{eq}$ è quindi possibile utilizzare un generatore di tensione di test.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Dalla rete si ricava che:
$\mathrm{Z_{eq}=\frac{B_{eq}}{A_{eq}-A_{v}}}$
Anche in questo caso è necessario calcolare $A_{eq}$ e $B_{eq}$ .
E' possibile, a tal scopo, utilizzare i risultati appena ricavati.
La matrice T di un solo condensatore vale:
$\mathrm{\mathbf{T}_{C}=}\mathrm{\left(\begin{array}{cc}\left.\frac{V_{1}}{V_{2}}\right|_{I_{2}=0} & \left.\frac{V_{1}}{I_{2}}\right|_{V_{2}=0}\\\left.\frac{I_{1}}{V_{2}}\right|_{I_{2}=0} & \left.\frac{I_{1}}{I_{2}}\right|_{V_{2}=0}\end{array}\right)}=\left(\begin{array}{cc}1 & 0\\\jmath\omega\mathrm{C} & 1\end{array}\right)$
Quindi:
$\mathrm{\mathbf{T_{eq}}=\left(\begin{array}{cc}A_{osc} & B_{osc}\\C_{osc} & D_{osc}\end{array}\right)\left(\begin{array}{cc}1 & 0\\-\jmath\omega C & 1\end{array}\right)}=\left(\begin{array}{cc}\mathrm{A_{osc}-\jmath\omega CB_{osc}} & \mathrm{B_{osc}}\\\boxtimes & \boxtimes\end{array}\right)$

Inserendo i valori trovati nella formula di $Z_{eq}$ si ricava che:
$\mathrm{Z_{eq}=\frac{V_{T}}{I_{T}}=\frac{\left(A_{osc}-A_{v}\right)B_{osc}}{\left(A_{osc}-A_{v}\right)^{2}+\left(\omega CB_{osc}\right)^{2}}+\jmath\frac{\omega CB_{osc}^{2}}{\left(A_{osc}-A_{v}\right)^{2}+\left(\omega CB_{osc}\right)^{2}}}$

Le considerazioni fattibili alla vista di queste formule sono che:

In condizioni di oscillazione [ 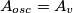$A_{osc}=A_{v}$ ] si ha che 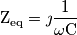$\mathrm{Z_{eq}=\jmath\frac{1}{\omega C}}$ in entrambi i casi;
In condizioni di oscillazione, la parte reattiva della formula è pari alla reattanza di un condensatore cambiata di segno. Questa è la firma di un gruppo LC in risonanza. Questo implica che TUTTI gli oscillatori, di qualunque natura e specie, sono equivalenti ad un gruppo LC portato alla risonanza;
La parte resistiva, in condizioni di oscillazione, è pari a zero. Questo è frutto di una compensazione tra una parte resistiva positiva (perdite del circuito) e una parte resistiva negativa (effetto dell'amplificatore);
I generatori di tensione e di corrente di test cortocircuitano e aprono, rispettivamente, la reazione. Un generico oscillatore può fare a meno della discussione in termini di sistema retroazionato.

Un qualunque oscillatore è quindi equivalente ad un oscillatore a resistenza negativa, a sua volta uguale ad un gruppo LC ideale.
poiché la reattanza di un induttore è pari a $\omega\mathrm{L}$ si può ricavare che, per un qualunque oscillatore la L o è reale oppure è simulata secondo la relazione:
$\mathrm{X_{eq}=\left.\frac{1}{\omega C}\right|}_{\omega=\frac{1}{kRC}}\Rightarrow\mathrm{X_{eq}=kR}=\omega\mathrm{L=\frac{L}{kRC}\Rightarrow L=k^{2}R^{2}C}$ .
Per esempio, per un oscillatore a sfasamento si ha che $\omega=\frac{1}{\sqrt{6}\mathrm{RC}}$ quindi $k=\sqrt{6}$ e $\mathrm{L=6}\mathrm{R^{2}C}$ .
Si deve notare che k potrebbe non essere unico. Un caso è l'oscillatore a sfasamento con i tre blocchi T diversi tra loro. In questo caso si può ricavare, in generale, che $\omega=\frac{1}{\sqrt{{\sum_{i=0}^{dim(k)}}\mathrm{\left(k_{i}R_{i}C_{i}\right)^{2}}}}$ .

*FINE*
PS: scusate se il post è diventato un po' lungo... :-P

da **IsidoroKZ** » 17 set 2012, 20:45

ARTICOLO!

da **jordan20** » 17 set 2012, 20:57

IsidoroKZ ha scritto:ARTICOLO!

Assolutamente :!:

da **DirtyDeeds** » 17 set 2012, 21:02

Ciumbia che roba! Complimenti!

Chiedo anch'io a gran voce un

ARTICOLO!

PietroBaima ha scritto:[Dove mi sono conformato all'uso della j in luogo della i per indicare il versore complesso in auge tra gli elettronici, di cui non faccio parte ]

Per altri aggiustamenti notazionali (ce ne sono un paio da fare), passa in segreteria ;-)