Durante una delle prime lezioni di elettronica analogica si cerca di spiegare gli stimoli sinusoidali per un condensatore ed una induttanza.
Considerato

In un condensatore si osserva che:

In una induttanza invece:

risolvendo l'integrale si ottiene così l'equazione

da cui

di tutto questo però, probabilmente per mie lacune, non riesco a spiegarmi l'equazione
 che mi porta al risultato ottenuto. Come faccio ad ottenere l'uguaglianza tra coseno e jseno?
che mi porta al risultato ottenuto. Come faccio ad ottenere l'uguaglianza tra coseno e jseno?Grazie.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)
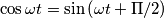 per cui la
per cui la  anteposta rappresenta lo sfasamento di
anteposta rappresenta lo sfasamento di 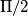


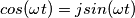 non mi sembra corretta perché :
non mi sembra corretta perché :  e
e 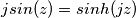 ma
ma 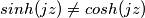 (inoltre si avrebbe che la funzione
(inoltre si avrebbe che la funzione 
 ).
).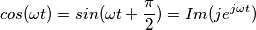 .
.

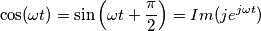 secondo te
secondo te 

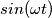 non dovrebbe essere un fasore; secondo me le formule del post 1 non sono del tutto corrette perché risulterebbe che la corrente del condensatore
non dovrebbe essere un fasore; secondo me le formule del post 1 non sono del tutto corrette perché risulterebbe che la corrente del condensatore  e la tensione dell'induttore
e la tensione dell'induttore 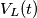 sarebbero funzioni a valori complessi. Secondo me è stato sovrapposto il modo di procedere con i fasori alla trattazione "nel tempo".
sarebbero funzioni a valori complessi. Secondo me è stato sovrapposto il modo di procedere con i fasori alla trattazione "nel tempo". per il condensatore mentre è in ritardo sempre di
per il condensatore mentre è in ritardo sempre di 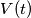 (funzione del tempo) e non la
(funzione del tempo) e non la  (nel senso di fasore). Se non ho capito male, j rappresenta un operatore che aumenta di
(nel senso di fasore). Se non ho capito male, j rappresenta un operatore che aumenta di 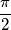 la fase di una sinusoide (o cosinusoide) solo nel dominio dei fasori; quello che intendevo dire è che secondo me le ultime due uguaglianze di quella formula non sono corrette
la fase di una sinusoide (o cosinusoide) solo nel dominio dei fasori; quello che intendevo dire è che secondo me le ultime due uguaglianze di quella formula non sono corrette