^=negato
scrivere la somma canonica
Moderatori: ![]() carloc,
carloc, ![]() g.schgor,
g.schgor, ![]() BrunoValente,
BrunoValente, ![]() IsidoroKZ
IsidoroKZ
8 messaggi
• Pagina 1 di 1
0
voti
Buongiorno... oggi ho una domanda semplice semplice..come si scrive la somma canonica di una funzione?? so che la somma canonica è la somma dei mintermini, e se mi si da una tabella della verità, so come si fa... ma se invece mi danno una funzione F = A^B ^ + (A^ + D^) (B + (D^C^)).. come si scrive la somma canonica?? e poi per trovare la somma minima, devo partire da questa funzione, o da quella trovata tramite la somma canonica?? ringrazio in anticipo 
^=negato
^=negato
0
voti
Non vorrei sbagliarmi, dato che non rivedo questi concetti da un po' di tempo, tuttavia credo che potresti procedere in questo modo...
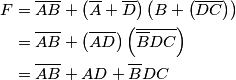
Attendi il parere di altri utenti oppure puoi verificare da te se le due funzioni logiche coincidono
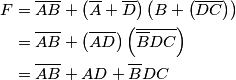
Attendi il parere di altri utenti oppure puoi verificare da te se le due funzioni logiche coincidono
Emanuele Lorina
- Chi lotta contro i mostri deve fare attenzione a non diventare lui stesso un mostro. E se tu riguarderai a lungo in un abisso, anche l'abisso vorrà guardare dentro di te (F. Nietzsche)
- Tavole della legge by admin
- Chi lotta contro i mostri deve fare attenzione a non diventare lui stesso un mostro. E se tu riguarderai a lungo in un abisso, anche l'abisso vorrà guardare dentro di te (F. Nietzsche)
- Tavole della legge by admin
-

 Lele_u_biddrazzu
Lele_u_biddrazzu
8.154 3 8 13 - Master EY

- Messaggi: 1288
- Iscritto il: 23 gen 2007, 16:13
- Località: Modena
0
voti
ma hai semplicemente applicato "de Morgan"?
è così che si fa la somma canonica??
è così che si fa la somma canonica??
0
voti
Per ottenere la somma canonica, se non ricordo male, devi prima ricavare la tabella di verità  In effetti prima ho applicato i teoremi di De Morgan, ottenendo una semplificazione delle funzione logica. Buon lavoro
In effetti prima ho applicato i teoremi di De Morgan, ottenendo una semplificazione delle funzione logica. Buon lavoro 
edit: dimenticavo... per ricavare la forma minima della funzione logica dovresti utilizzare le mappe di Karnaugh... ho provato a cimentarmi ottenendo questo risultato...
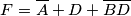
Chiaramente lascio a te verificare la bontà del risultato perché è probabile che abbia tralasciato qualcosa per strada...
edit: dimenticavo... per ricavare la forma minima della funzione logica dovresti utilizzare le mappe di Karnaugh... ho provato a cimentarmi ottenendo questo risultato...
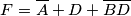
Chiaramente lascio a te verificare la bontà del risultato perché è probabile che abbia tralasciato qualcosa per strada...
Emanuele Lorina
- Chi lotta contro i mostri deve fare attenzione a non diventare lui stesso un mostro. E se tu riguarderai a lungo in un abisso, anche l'abisso vorrà guardare dentro di te (F. Nietzsche)
- Tavole della legge by admin
- Chi lotta contro i mostri deve fare attenzione a non diventare lui stesso un mostro. E se tu riguarderai a lungo in un abisso, anche l'abisso vorrà guardare dentro di te (F. Nietzsche)
- Tavole della legge by admin
-

 Lele_u_biddrazzu
Lele_u_biddrazzu
8.154 3 8 13 - Master EY

- Messaggi: 1288
- Iscritto il: 23 gen 2007, 16:13
- Località: Modena
0
voti
e questo è il problema.. come ricavare la tabella di verità..
0
voti
Ah... non è difficile prendi la versione semplificata della funzione logica e la utilizzi per ricavarne l'uscita in corrispondenza di tutte le possibili combinazioni degli ingressi  Prova, vedrai che non è così difficile come sembra
Prova, vedrai che non è così difficile come sembra 
Emanuele Lorina
- Chi lotta contro i mostri deve fare attenzione a non diventare lui stesso un mostro. E se tu riguarderai a lungo in un abisso, anche l'abisso vorrà guardare dentro di te (F. Nietzsche)
- Tavole della legge by admin
- Chi lotta contro i mostri deve fare attenzione a non diventare lui stesso un mostro. E se tu riguarderai a lungo in un abisso, anche l'abisso vorrà guardare dentro di te (F. Nietzsche)
- Tavole della legge by admin
-

 Lele_u_biddrazzu
Lele_u_biddrazzu
8.154 3 8 13 - Master EY

- Messaggi: 1288
- Iscritto il: 23 gen 2007, 16:13
- Località: Modena
3
voti
giusi ha scritto:... ma se invece mi danno una funzione F = A^B ^ + (A^ + D^) (B + (D^C^)).. come si scrive la somma canonica??
Direi che per scrivere la funzione logica in forma canonica come somma di prodotti ti basterebbe andare a sviluppare la forma iniziale scrivendo

e quindi andando ad individuare sulla mappa di Karnaugh i vari termini al fine di settarli ad uno;
fatto ciò avresti a disposizione tutti i singoli minterm da addizionare nella SOP

ma, prima di usare la K-map, avresti potuto anche cercare di semplificare ancora un po' la funzione, con un ulteriore passaggio ricordando che, grazie a complementarità e assorbimento, i primi tre termini si possono ridurre ad un unico A negato

giusi ha scritto: e poi per trovare la somma minima, devo partire da questa funzione, o da quella trovata tramite la somma canonica??
Una volta scritta la K-map puoi cercare anche la somma minima, cercando gli implicanti primi essenziali
ottenendo

ma vedi che anche usando un po' di algebra di Boole, a volte ci si riesce ugualmente, anche se, senza ombra di dubbio, la semplificazione si "vede" meglio nella K-map.
"Il circuito ha sempre ragione" (Luigi Malesani)
1
voti
wow, risposta più chiara di così non si può chiedere!! grazie mille a entrambi, è molto semplice, ma sui libri non sono riuscita a trovare come si fa... tante grazie veramente  buon week end
buon week end 
8 messaggi
• Pagina 1 di 1
Chi c’è in linea
Visitano il forum: Nessuno e 30 ospiti

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)




