è possibile risolvere questo integrale?

grazie
Moderatori: ![]() PietroBaima,
PietroBaima, ![]() Ianero
Ianero

elettrobit ha scritto:Non mi trovo solamente con gli estremi di integrazione del primo integrale (quello non appena è stata fatta la sostituzione); dovrebbe essere da t a 0.
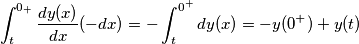
Visitano il forum: Nessuno e 11 ospiti