e voglio trovare il segnale di ingresso che rende infinita tale impedenza allora ho che l'ammettenza del bipolo nel dominio trasformato è

se il segnale di ingresso è un esponenziale

allora

quindi se

allora

quindi antitrasformando

quello che non capisco (ammesso che il procedimensto sia corretto..ma penso di si) è come mai la corrente trasformata viene CV quindi dimensionalmente una carica e non una corrente.Qualcuno sa darmi una mano? Grazie

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



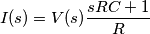
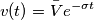 la corrente diventa
la corrente diventa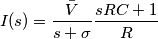
 che carica istantaneamente la capacità: se calcoli l'integrale di corrente ottieni infatti
che carica istantaneamente la capacità: se calcoli l'integrale di corrente ottieni infatti
 , quindi non vedrai entrare altra corrente nel circuito.
, quindi non vedrai entrare altra corrente nel circuito.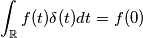 che ha ovviamente le dimensioni di
che ha ovviamente le dimensioni di  , quindi
, quindi  è dimensionalmente l'inverso di un tempo, ossia ha come dimensione l'Hz, però non saprei dimostrartelo a partire dalla definizione, forse considerandolo come
è dimensionalmente l'inverso di un tempo, ossia ha come dimensione l'Hz, però non saprei dimostrartelo a partire dalla definizione, forse considerandolo come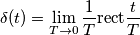
 ha una dimensione
ha una dimensione ![[As] [As]](/forum/latexrender/pictures/bd5d59a47111589b12e7c2d29cbe4ac8.png) in quanto una corrente è stata integrata nel tempo dall'operatore della trasformata. Per questo motivo penso che portando
in quanto una corrente è stata integrata nel tempo dall'operatore della trasformata. Per questo motivo penso che portando  al secondo membro le dimensioni dovrebbero tornare.
al secondo membro le dimensioni dovrebbero tornare. 

