Così come posta, la richiesta dell'esercizio non mi è chiarissima. Forse sarò arrugginito io...
 wackos ha scritto:
wackos ha scritto:Devo individuare i punti di

dove gli insieme di livello di

hanno tangente a 45 gradi rispetto alle x positive...
A seconda delle interpretazioni, per me, la precedente frase potrebbe significare tutto o niente.
Mi spiego.
Quando si lavora con funzioni di singola variabile, ad essere più precisi funzioni del tipo
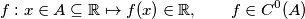
con

aperto, se si chiede di trovare la "tangente" in un punto

(con

) non ci possono essere ambiguità in quanto di tangente (alla curva descritta da f nel piano xy) passante per

c'è solamente una retta

.
Per esempio, se

è un intervallo, la situazione è la seguente
Si trova facilmente che l'equazione (di possibile interesse) che descrive la tangente è la seguente:

Quando si passa dallo spazio a due dimensioni, nel quale vivono le funzioni di singola variabile, allo spazio a tre dimensioni, nel quale invece vivono le funzioni di due variabili della forma

(sempre con

aperto) le cose diventano ambigue. Infatti se adesso fissiamo un qualsiasi punto

abbiamo che per il punto

non passa più solamente un'unica retta tangente (alla superficie descritta da f nello spazio xyz), ma infinite.
Ma non è finita, date le precedenti circostanze, risulta ben definito anche un piano tangente (sempre alla superficie descritta da f) passante per il solito punto

.
Una possibile situazione potrebbe essere la seguente
Per questioni di praticità ho riportato nell'esempio solo 2 rette tangenti e il piano tangente passanti per

.
L'equazione (di possibile interesse) che descrive il piano si trova abbastanza facilmente dopo qualche conto, e risulta essere

Se ora vogliamo tiriare in ballo anche gli insiemi di livello, dallo spazio 3-dimensionale si torna allo spazio 2-dimensionale.
Gli insiemi di livello

di una funzione di due variabili, non sono altro che gli insiemi di punti che verificano una relazione del tipo

In genere tali insiemi di punti rappresentano una curva nel piano a quota k e parallelo a al piano xy (cioè il piano z=k).
In certi casi (vedi il teorema del Dini per un criterio necessario) tale curva può essere espressa in una delle seguenti forme esplicite


inoltre, se vale il teorema del Dini, tale curva risulta essere di classe

, dunque nel caso in cui è possibile trovare le funzioni

e

ha perfettamente senso andare studiare il comportamento delle sue tangenti (che sono rette, dato che siamo tornati in 2 dimensioni).
Dunque, in sostanza, la mia domanda è: tra tutte le possibili tangenti che si hanno nei problemi a 3 dimensioni, quali vuoi trovare?
wackos ha scritto:Devo individuare i punti di

dove gli insieme di livello di

hanno tangente a 45 gradi rispetto alle x positive...
Intanto, "per punti di

" intendi punti del piano xy?
Poi, "dove gli insieme di livello di

hanno tangente a 45 gradi rispetto alle x positive", per me, non ha proprio alcun senso.
Un angolo si definisce tramite due rette incidenti, quindi un insieme di livello (che, come già detto, è una particolare curva) non può "avere tangente a 45 gradi rispetto alle x positive".
Se non hai compreso bene la richiesta dell'esercizio, prova a riportare alla lettera il testo "ufficiale", in modo da mettere me e gli altri utenti del forum nelle condizioni di interpretare bene il problema, al fine di indirizzarti alla corretta soluzione.
 dove gli insieme di livello di
dove gli insieme di livello di 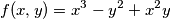 hanno tangente a 45 gradi rispetto alle x positive...
hanno tangente a 45 gradi rispetto alle x positive...
 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



![\[\mathbb{R}^{2}\] \[\mathbb{R}^{2}\]](/forum/latexrender/pictures/3c2cb218b8e32b7fb0e0f8909ae23eff.png) per la medesima funzione
per la medesima funzione ![\[f(x,y)=x^3-y^2+x^2y\] \[f(x,y)=x^3-y^2+x^2y\]](/forum/latexrender/pictures/75ac59918c3a62ef08370aa5ffddf327.png)
![\[y'(x)= \tan \left ( \frac{\pi }{4} \right )=1\] \[y'(x)= \tan \left ( \frac{\pi }{4} \right )=1\]](/forum/latexrender/pictures/83cf070f6aa34cfa11261df825101907.png)
![\[y'(x)=\frac{\mathrm{dy} }{\mathrm{d} x}\] \[y'(x)=\frac{\mathrm{dy} }{\mathrm{d} x}\]](/forum/latexrender/pictures/c5cb2e2f08d91ca8a5ba2f91b28e7350.png)
![\[\frac{\pi }{4}\] \[\frac{\pi }{4}\]](/forum/latexrender/pictures/bbe5156762c5ba923fc56d8fb9773f9f.png) li vai a sostituire in
li vai a sostituire in 
 come parametro e risolvere l'equazione in
come parametro e risolvere l'equazione in  .
. hanno tangente a 45 gradi rispetto alle x positive...
hanno tangente a 45 gradi rispetto alle x positive...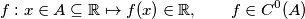
 aperto, se si chiede di trovare la "tangente" in un punto
aperto, se si chiede di trovare la "tangente" in un punto  (con
(con  ) non ci possono essere ambiguità in quanto di tangente (alla curva descritta da f nel piano xy) passante per
) non ci possono essere ambiguità in quanto di tangente (alla curva descritta da f nel piano xy) passante per  .
.


 abbiamo che per il punto
abbiamo che per il punto  non passa più solamente un'unica retta tangente (alla superficie descritta da f nello spazio xyz), ma infinite.
non passa più solamente un'unica retta tangente (alla superficie descritta da f nello spazio xyz), ma infinite.

 di una funzione di due variabili, non sono altro che gli insiemi di punti che verificano una relazione del tipo
di una funzione di due variabili, non sono altro che gli insiemi di punti che verificano una relazione del tipo 


 , dunque nel caso in cui è possibile trovare le funzioni
, dunque nel caso in cui è possibile trovare le funzioni  e
e  ha perfettamente senso andare studiare il comportamento delle sue tangenti (che sono rette, dato che siamo tornati in 2 dimensioni).
ha perfettamente senso andare studiare il comportamento delle sue tangenti (che sono rette, dato che siamo tornati in 2 dimensioni).

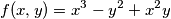 hanno una tangente a
hanno una tangente a 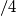 rispetto alle
rispetto alle  ''
''