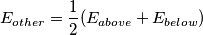Un nuovo esempio è la dimostrazione del valore della pressione elettrostatica sulla superficie dei conduttori:

Per dimostrarla il libro considera una superficie conduttrice, forandola in modo da perturbare di poco il campo.

Il libro approssima la parte mancante come un piano, il cui campo generato sulla superficie è:

(Questo risultato era stato ottenuto in precedenza per un piano infinito, non infinitesimo. Sta barando
Sulla superficie del resto della sfera si ha:

per cui:

Infine:

Dimostrazione conclusa.
Ora io mi chiedo perché tutto questo casino nel bucare la superficie e barare con quel piano approssimante.
Potrei benissimo ragionare con le stesse linee di principio ottenendo però un risultato diverso, non seguendo i suoi passaggi.
Considero una superficie generica e so che in un punto della sua superficie per il teorema di Coulomb ho che il campo vale:

che corrisponde al campo generato da tutte le altre cariche della superficie nel punto considerato.
Se in quel punto è presente quel campo allora la carica superficiale in quel punto sentirà una pressione pari a:

La densità superficiale è infatti una grandezza che varia da punto a punto, non vedo perché sia necessario togliere alla superficie un pezzetto di essa (approssimandola pure), anziché un punto, come in questo caso, ottenendo però un risultato doppio di quello desiderato.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)




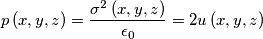
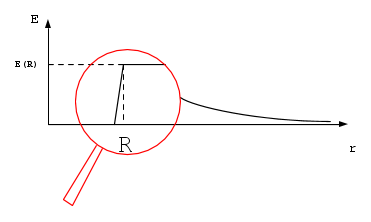
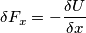
 ... tiny enough so it is essentially flat ..."
... tiny enough so it is essentially flat ..."