 da
da  PietroBaima » 1 dic 2014, 2:39
PietroBaima » 1 dic 2014, 2:39
Vicentio ha scritto:la formula di Heremit
Hermite si è trasferito in punta ad una montagna perché voleva stare solo?

Scherzo

Anyway, questo thread mi è utile per mostrare un
tool per il matematico
cool.
Quando si hanno delle funzioni da integrare che sono delle potenze di integrali noti, si può cercare una formula di integrazione ricorsiva. Vado a spiegare il metodo, che usa l'integrazione per parti.
Il nucleo ricorsivo della nostra formula è:

Proviamo ad integrare per parti la funzione potenza n-esima del nostro nucleo ricorsivo:

Assumo:

da cui:

e

da cui:

trovo che:

da cui:



adesso "arretro" n di una posizione, in modo da avere una ricorsione comoda all'indietro:

Nota: La formula non è in grado di risolvere il nucleo ricorsivo, per il quale la soluzione va trovata per altra via (basta provare a porre n=1 per rendersene conto).
Poniamo n=2, per esempio



Vediamo anche il caso n=3

![\int \frac{1}{(1+x^2)^{3}}\mathrm{d}x=\frac{3}{4} \left[ \frac{1}{2}\arctan(x)+ \frac{1}{2}\ \frac{x}{1+x^2}\right ]+ \frac{1}{4}\frac{x}{(1+x^2)^{2}}+c \int \frac{1}{(1+x^2)^{3}}\mathrm{d}x=\frac{3}{4} \left[ \frac{1}{2}\arctan(x)+ \frac{1}{2}\ \frac{x}{1+x^2}\right ]+ \frac{1}{4}\frac{x}{(1+x^2)^{2}}+c](/forum/latexrender/pictures/d0ed3848f89261454319c1433ff66a8f.png)
...
Per "srotolare" la formula ricorsiva e scriverne una diretta conviene usare le ipergeometriche, ma direi che qui non sia proprio il caso.
Ciao,
Pietro.
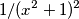 ?
?![]() PietroBaima,
PietroBaima, ![]() Ianero
Ianero
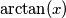 mentre la seconda è quasi come prima.
mentre la seconda è quasi come prima.













![\int \frac{1}{(1+x^2)^{3}}\mathrm{d}x=\frac{3}{4} \left[ \frac{1}{2}\arctan(x)+ \frac{1}{2}\ \frac{x}{1+x^2}\right ]+ \frac{1}{4}\frac{x}{(1+x^2)^{2}}+c \int \frac{1}{(1+x^2)^{3}}\mathrm{d}x=\frac{3}{4} \left[ \frac{1}{2}\arctan(x)+ \frac{1}{2}\ \frac{x}{1+x^2}\right ]+ \frac{1}{4}\frac{x}{(1+x^2)^{2}}+c](/forum/latexrender/pictures/d0ed3848f89261454319c1433ff66a8f.png)

