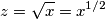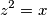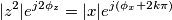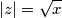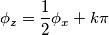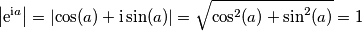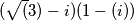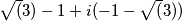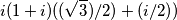![i(1+i)e^{i[ \pi/6]} i(1+i)e^{i[ \pi/6]}](/forum/latexrender/pictures/1fa4eb2457497479555d825e382a7f72.png)
Nel primo caso il modulo mi viene 0 mentre dovrebbe risultare

Mel secondo caso il modulo mi viene
 mentre dovrebbe essere
mentre dovrebbe essere 
Ho già rifatto entrambi almeno 30 volte e mi risultano sempre così , potreste aiutarmi? Non saprei proprio che altro fare per capire dove sbaglio :/ grazie mille

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

![\left|\text{i}(1+\text{i})e^{\text{i}[ \pi/6]}\right|= \left|\text{i}(1+\text{i})e^{\text{i}[ \pi/6]}\right|=](/forum/latexrender/pictures/cdeab8636125e72b06579ee0a6add57c.png)
![=\left|\text{i}\right|\left|1+\text{i}\right|\left|e^{\text{i}[ \pi/6]}\right|= =\left|\text{i}\right|\left|1+\text{i}\right|\left|e^{\text{i}[ \pi/6]}\right|=](/forum/latexrender/pictures/3deda53ac25f83d527b3b1d836432c5e.png)
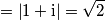
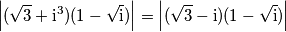
 pigreco]=π
pigreco]=π

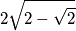


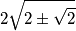 .
.