1-2+3-4+5-6+... +
1-2+3-4+5-... =
1-1+1-1+1-1+... = 0.5
Da cui: 1-2+3-4+5-6+... = 0.25
E se facessi così?
1-2+3-4+5-6+... = 1+(-2+3)+(-4+5)+... = 1+1+1+1+1+... = 0.25
1-2+3-4+5-6+... = (1-2)+(3-4)+(5-6)+... = -1-1-1-1-1-... = 0.25
0.25 = -0.25
Moderatori: ![]() PietroBaima,
PietroBaima, ![]() Ianero
Ianero




 facendo alcuni errori (su cose che all'epoca non erano ancora chiarite).
facendo alcuni errori (su cose che all'epoca non erano ancora chiarite). , quindi ponendo z=-1 ottengo la somma di tutti i naturali) fa proprio... -1/12
, quindi ponendo z=-1 ottengo la somma di tutti i naturali) fa proprio... -1/12 

PietroBaima ha scritto:
 si intendono proprio i numeri naturali? E quel
si intendono proprio i numeri naturali? E quel 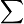 indica proprio la somma?
indica proprio la somma?sebago ha scritto:COSA?
sebago ha scritto:ma persi intendono proprio i numeri naturali?
sebago ha scritto:E quelindica proprio la somma?
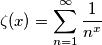
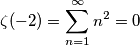
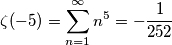
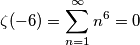
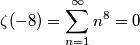
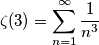
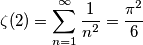


Visitano il forum: Nessuno e 11 ospiti