Purtroppo le lezioni del corso sono state tenute "alla meno peggio" con dei lucidi molto approssimativi, di cui nessuno di noi seguenti è in possesso.
Non ci è stata data neanche un bibliografia per andare a ricercare gli argomenti trattati. In sostanza mi ritrovo ad affrontare una materia nuova senza alcun riferimento da seguire e con degli appunti pessimi.
Mi scuso quindi in anticipo per gli sfondoni che quasi sicuramente scriverò.
Dunque, vengo al punto. Ho provato a risistemare gli appunti, però come risultato trovo un paio di contraddizioni da risolvere. Provo a esporre quanto ho capito fin ora.
Legge di Rayleigh
Quando un'onda elettromagnetica incide su di un corpo questa subisce una attenuazione che obbedisce alla legge di Lambert-Beer-Bouguer

dove
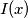 indica l'intensità dell'onda (in radiometria misurata in
indica l'intensità dell'onda (in radiometria misurata in 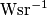 ) ad una data distanza
) ad una data distanza  dall'interfaccia tra il mezzo di propagazione e il corpo;
dall'interfaccia tra il mezzo di propagazione e il corpo; è l'intensità dell'onda all'interfaccia;
è l'intensità dell'onda all'interfaccia; è il coefficiente di attenuazione associato al corpo investito dall'onda.
è il coefficiente di attenuazione associato al corpo investito dall'onda.

dove
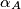 è il coefficiente di assorbimento, proporzionale a
è il coefficiente di assorbimento, proporzionale a 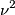 (con
(con  frequenza dell'onda incidente), che tiene conto della porzione di in energia elettromagnetica dell'onda convertita in calore;
frequenza dell'onda incidente), che tiene conto della porzione di in energia elettromagnetica dell'onda convertita in calore; è il coefficiente di diffusione (o di scattering), proporzionale a
è il coefficiente di diffusione (o di scattering), proporzionale a 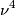 .
.
 dalla potenza quarta della frequenza dell'onda è la legge di diffusione di Rayleigh.
dalla potenza quarta della frequenza dell'onda è la legge di diffusione di Rayleigh.Diffusione
Detta
 la lunghezza dell'onda incidente e
la lunghezza dell'onda incidente e  il diametro delle particelle che costituiscono il corpo investito dalla radiazione si ha che
il diametro delle particelle che costituiscono il corpo investito dalla radiazione si ha che- se
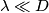 allora il fenomeno dominante è l'assorbimento (e riflessione) dell'onda;
allora il fenomeno dominante è l'assorbimento (e riflessione) dell'onda; - se
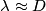 allora il fenomeno dominante è la diffusione dell'onda;
allora il fenomeno dominante è la diffusione dell'onda; - se
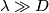 allora il corpo risulta trasparente all'onda.
allora il corpo risulta trasparente all'onda.
Qua c'è la prima contraddizione, in quanto in base a quanto detto riguardo il coefficiente di attenuazione si ha che in alta frequenza conta la diffusione mentre in bassa frequenza conta l'assorbimento.
Il problema si risolverebbe se fosse vero che il coefficiente di assorbimento dipende dalla frequenza secondo una potenza di esponente maggiore di quattro.
Banda ottica di un fotorivelatore
L'energia radiante associata ad un'onda elettromagnetica, misurata in
 , costituita da
, costituita da  "fasci" [è il termine giusto?] di fotoni di frequenza distinta , è data da
"fasci" [è il termine giusto?] di fotoni di frequenza distinta , è data da 
dove
 è la costante di Plank;
è la costante di Plank; è il numero di fotoni che costituisco il fascio luminoso di frequenza
è il numero di fotoni che costituisco il fascio luminoso di frequenza 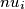 .
.
in particolare, quando l'onda è costituita da un unico fotone la precedente relazione si riduce alla seguente

Conseguentemente il flusso (o potenza) radiante dell'onda, in
 , è dato da
, è dato da
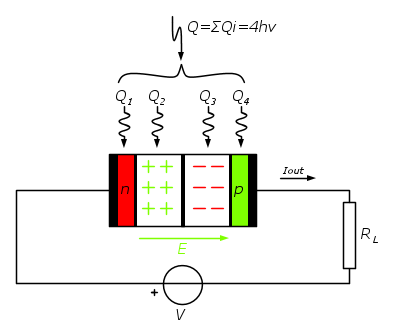
Quando un fotorivelatore (connesso opportunamente in un circuito elettrico) è investito da una radiazione questo può rispondere generando una corrente elettrica continua. L'intensità
 di tale corrente, in
di tale corrente, in  , quando il fotorivelatore è investito da un'onda monocromatica, è descritta dall'equazione base dei fotoconduttori
, quando il fotorivelatore è investito da un'onda monocromatica, è descritta dall'equazione base dei fotoconduttori
dove
 è la carica dell'elettrone;
è la carica dell'elettrone; tiene conto del rendimento del fotorivelatore [è l'efficienza quantica?], nel senso che quantifica il fatto che solo una parte dei fotoni assorbiti generano carica elettrica (i restanti vengono trasformati in calore);
tiene conto del rendimento del fotorivelatore [è l'efficienza quantica?], nel senso che quantifica il fatto che solo una parte dei fotoni assorbiti generano carica elettrica (i restanti vengono trasformati in calore);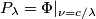 è la potenza dell'onda monocromatica;
è la potenza dell'onda monocromatica; è la mobilità degli elettroni;
è la mobilità degli elettroni; è la tensione a cui è sottoposto il fotorivelatore;
è la tensione a cui è sottoposto il fotorivelatore; è la velocità della luce;
è la velocità della luce;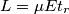 è una lunghezza legata al campo elettrico
è una lunghezza legata al campo elettrico  interno al fotorivelatore e il tempo di attraversamento
interno al fotorivelatore e il tempo di attraversamento  [cosa indica il pedice?] impiegato dai portatori di carica per attraversare il fotorivelatore.
[cosa indica il pedice?] impiegato dai portatori di carica per attraversare il fotorivelatore.
La
 è valida fintanto che la potenza ottica incidente è sufficiente per generare portatori di carica liberi nel fotorivelatore. Più precisamente, detta
è valida fintanto che la potenza ottica incidente è sufficiente per generare portatori di carica liberi nel fotorivelatore. Più precisamente, detta  l'energy gap associata al materiale costituente il fotorivelatore, l'equazione
l'energy gap associata al materiale costituente il fotorivelatore, l'equazione  è valida se risulta verificata la condizione
è valida se risulta verificata la condizione
da cui si deduce che il fotorivelatore è in grado di risolvere radiazioni di lunghezza d'onda

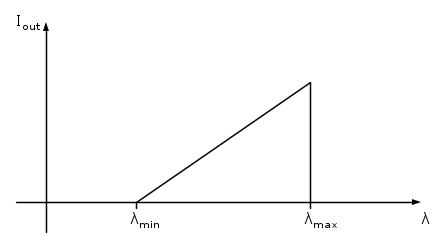
Si conclude quindi che la caratteristica corrente/lunghezza d'onda di un fotorivelatore, che descrive la sua banda ottica, è la seguente
L'andamento lineare è dovuto dalla
 , la soglia superiore dalla
, la soglia superiore dalla  mentre la soglia inferiore dalla legge di Rayleigh.
mentre la soglia inferiore dalla legge di Rayleigh.Ancora il discorso non torna. Secondo il ragionamento riguardante la diffusione arrivo a concludere nuovamente che (in accordo alla
 ) esiste una soglia superiore, dovuta ancora al fatto che al di sopra di una certa
) esiste una soglia superiore, dovuta ancora al fatto che al di sopra di una certa  un qualsiasi fotorivelatore non riesce ad assorbire potenza dalla radiazione incidente.
un qualsiasi fotorivelatore non riesce ad assorbire potenza dalla radiazione incidente.Niente giustifica l'esistenza di una soglia inferiore
 .
.Probabilmente mi sto perdendo in un bicchier d'acqua.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)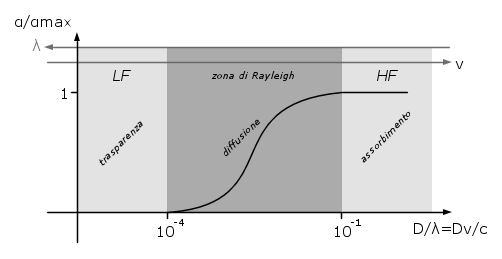


 instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.


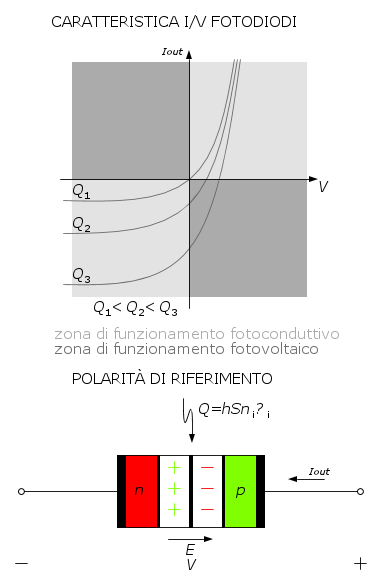
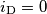 se si vuole una risposta logaritmica (v.
se si vuole una risposta logaritmica (v. 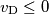 , il fotodiodo opera in modalità fotoconduttiva. Nel quarto quadrante, in modalità fotovoltaica.
, il fotodiodo opera in modalità fotoconduttiva. Nel quarto quadrante, in modalità fotovoltaica.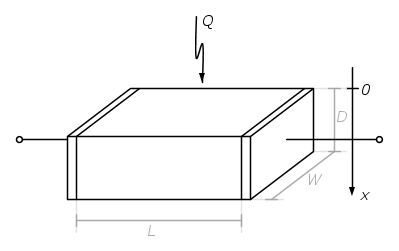

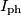 è l'intensità della corrente fotogenerata.
è l'intensità della corrente fotogenerata.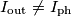 , ossia
, ossia 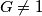 .
.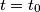 , la densità spaziale di carica libera
, la densità spaziale di carica libera  nel fotorivelatore segue la legge
nel fotorivelatore segue la legge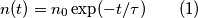
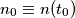 è la densità di carica spaziale iniziale;
è la densità di carica spaziale iniziale; è il
è il 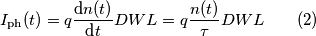
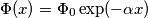
 è il flusso attraverso la superficie superiore del fotorivelatore.
è il flusso attraverso la superficie superiore del fotorivelatore.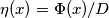 [la dipendenza da 1/D non l'ho capita, e poi a naso, dato che dovrebbe essere adimensionale, mi verrebbe più da dire che dipende direttamente da D...]
[la dipendenza da 1/D non l'ho capita, e poi a naso, dato che dovrebbe essere adimensionale, mi verrebbe più da dire che dipende direttamente da D...]![\begin{aligned}
n(x;t) &=\eta(x) n_0 \exp(-t/\tau) \\
&=\frac{\Phi_0\exp(-\alpha x)}{D} n_0 \exp(-t/\tau) \\
&=n_0 \frac{\Phi_0}{D} \exp[-(\alpha x + t/\tau)]
\end{aligned} \begin{aligned}
n(x;t) &=\eta(x) n_0 \exp(-t/\tau) \\
&=\frac{\Phi_0\exp(-\alpha x)}{D} n_0 \exp(-t/\tau) \\
&=n_0 \frac{\Phi_0}{D} \exp[-(\alpha x + t/\tau)]
\end{aligned}](/forum/latexrender/pictures/63d6f82d751677479d53c69d635b1e73.png)
![\begin{aligned}
I_\text{ph} (x;t) &= q \frac{n(x;t)}{\tau}DWL \\
&=q \frac{n_0 (\Phi_0 / D) \exp[-(\alpha x + t/ \tau)]}{\tau} DWL \\
&=q n_0 \Phi_0\frac{\exp[-(\alpha x + t/ \tau)]}{\tau}WL
\end{aligned} \begin{aligned}
I_\text{ph} (x;t) &= q \frac{n(x;t)}{\tau}DWL \\
&=q \frac{n_0 (\Phi_0 / D) \exp[-(\alpha x + t/ \tau)]}{\tau} DWL \\
&=q n_0 \Phi_0\frac{\exp[-(\alpha x + t/ \tau)]}{\tau}WL
\end{aligned}](/forum/latexrender/pictures/cd9877fcc0981641793181a3a33228d9.png)
![N_\lambda(x;t) \equiv \Phi_0\frac{\exp[-(\alpha x + t/ \tau)]}{\tau} N_\lambda(x;t) \equiv \Phi_0\frac{\exp[-(\alpha x + t/ \tau)]}{\tau}](/forum/latexrender/pictures/0095394f9ea49437d3454f5c24cd8a19.png)

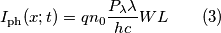
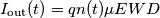
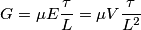
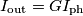
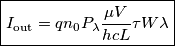
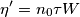 ).
).
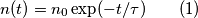
 di portatori di carica presenti nella zona fotosensibile sarà pari alla precedente densità spaziale moltiplicata per il volume
di portatori di carica presenti nella zona fotosensibile sarà pari alla precedente densità spaziale moltiplicata per il volume 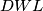 della zona fotosensibile del diodo, quindi
della zona fotosensibile del diodo, quindi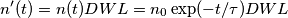
 presente nella zona fotosensibile del diodo, quindi
presente nella zona fotosensibile del diodo, quindi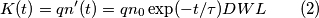
 [non è potenza radiante!]la densità superficiale di flusso del numero di fotoni, si ha che
[non è potenza radiante!]la densità superficiale di flusso del numero di fotoni, si ha che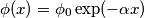
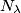 che fluiscono attraverso la sezione
che fluiscono attraverso la sezione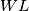 posta alla profondità
posta alla profondità 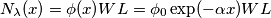
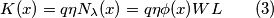
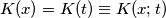
 ], dalla precedente uguaglianza si trova la seguente relazione
], dalla precedente uguaglianza si trova la seguente relazione 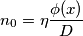
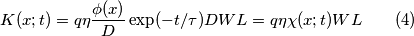
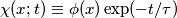
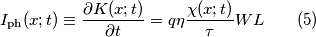
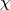 , corrisponde a
, corrisponde a 
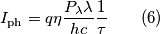
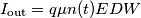
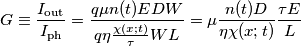
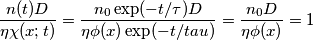
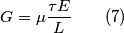
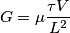
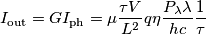
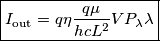

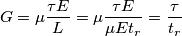
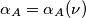 .
.