Ottima domanda
 novizio
novizio, la questione ha una certa rilevanza teorica nella teoria dei segnali, tanto è vero che in rete si trova molto materiale al riguardo . Se padroneggi la trasformata di Fourier non ti sarà difficile comprendere la trattazione matematica del campionamento
ZOH.
Conviene procedere andando a generalizzare per passi successivi il concetto di campionamento ideale.
Campionamento idealeSi consideri un segnale
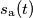 analogico
analogico, di
energia, in
banda base e
reale. Sotto queste ipotesi tale segnale e il suo campionamento (
regolare, ossia ottenuto campionato con periodo costante

, detto
tempo di campionamento) ammettono trasformata di Fourier.
Nel dominio del tempo il campionamento del segnale è una successione definita per mezzo dei suoi campioni. Di solito in letteratura si usa indicare l'n-esimo campione di un segnale analogico come
![s[n]:=s_\text{a}(nT_c), \qquad n\in\mathbb{Z} s[n]:=s_\text{a}(nT_c), \qquad n\in\mathbb{Z}](/forum/latexrender/pictures/0a657f8c61fa7eb42b1e6c8d58cb2610.png)
e non per mezzo della più familiare notazione

, utilizza pressoché sempre in analisi.
Tanto per capirsi la situazione è rappresentata nella seguente figura, raffigurante un generico segnale soddisfacente le precedenti ipotesi.
Il segnale campionato, a differenza del campionamento, è ancora un segnale analogico concentrato nei soli istanti di campionamento. Per la sua descrizione si ricorre all'utilizzo del
pettine di Dirac![\begin{aligned} s_c(t)&=\sum_{n\in\mathbb{Z}}s[n]\delta(t-nT_c) \\
&=\sum_{n\in\mathbb{Z}}s_a(t)\delta(t-nT_c)=s_a(t)\sum_{n\in\mathbb{Z}}\delta(t-nT_c) \end{aligned} \begin{aligned} s_c(t)&=\sum_{n\in\mathbb{Z}}s[n]\delta(t-nT_c) \\
&=\sum_{n\in\mathbb{Z}}s_a(t)\delta(t-nT_c)=s_a(t)\sum_{n\in\mathbb{Z}}\delta(t-nT_c) \end{aligned}](/forum/latexrender/pictures/580e02baabac30311b14262275152d6d.png)
tra terzo e quarto membro si è utilizzato la proprietà di campionamento della delta di Dirac.
Il segnale campionato è un segnale analogico, per cui, anche grazie alla precedenti ipotesi, si può passare ad una descrizione in frequenza trasformando secondo Fourier. Indicando con

la trasformata di Fourier (ossia lo
spettro) del segnale

, si trova

dove

indica il ben noto prodotto di convoluzione. Tra primo e secondo membro si è utilizzato il
teorema di convoluzione nel dominio della frequenza.
Il risultato che si è trovato è che, in condizioni ideali (campionamento regolare e istantaneo) lo spettro del segnale campionato, ossia

, è, a meno del fattore di scala

, dato dalla sovrapposizione di infinite repliche
esatte dello spettro del segnale da campionare (

), tutte centrate in multipli della
frequenza di campionamento 
.
Da questo risultato si deduce anche il
teorema del campionamento di Shannon.
Tanto per fissare le idee, supponiamo (ad esempio) che il segnale analogico di partenza abbia spettro
triangolare e banda

, cioè

Supponiamo inoltre che siano soddisfatte le ipotesi del teorema di campionamento, ad esempio per

, allora lo spettro del segnale campionato è il seguente:
Per ricostruire
esattamente il segnale di partenza è sufficiente filtrare una qualsiasi singola replica e riscalarla di un fattore

.
Campionamento naturaleSi abbandoni adesso l'ipotesi di campionamento istantaneo. Nel campionamento naturale non si prelevano punti della curva da campionare, ma bensì degli archi di una durata

, sempre con cadenza regolare di periodo

.
Si seguono gli stessi passi fatti nel caso precedente, con la sola, ma importante, differenza che il treno di impulsi viene sostituito con un treno di impulsi
rettangolari di durata finita

centrati agli istanti di campionamento

.
Passando al dominio della frequenza si trova

la funzione
sinc è il seno circolare.
La bontà teorica di tale campionamento è pari a quella del campionamento ideale, comunque presenta una sostanziale differenza.
In questo caso, come nel precedente, lo spettro del segnale campionato è dato dalla sovrapposizione di infinite repliche dello spettro del segnale di partenza. La differenza consiste che adesso ogni replica, pur sempre conservando la forma (e quindi il contenuto informativo) dello spettro di partenza, è riscalata di un fattore comune

e allo stesso tempo di un fattore proprio

.
Questo significa che, sempre in assenza di aliasing, adesso lo spettro del segnale campionato sarà qualcosa del genere
la curva inviluppo in chiaro è il prolungamento continuo di

, ossia

.
Ancora, è possibile ricostruire
esattamente il segnale originale filtrando una qualsiasi replica per poi riscalaral di un fattore opportuno.
Campionamento ZOHNel campionamento ZOH, a differenza del campionamento naturale, gli archi di campionamento vengono sostituiti da segmenti orizzontali.
In questo ultimo caso il segnale campionato assume la seguente espressione
![s_\text{c}(t)=\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right) s_\text{c}(t)=\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right)](/forum/latexrender/pictures/7f589de1135e50bd578a05b51fa11aaf.png)
che può essere riscritta nel seguente modo
![\begin{aligned}s_\text{c}(t) =\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right) &=\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right)*\delta(t-n T_c) \\
&=\sum_{n\in\mathbb{Z}}s_\text{a}[n]\delta(t-n T_c)* \text{rect}\left(\frac{t-nT_c}{\tau}\right)
\end{aligned} \begin{aligned}s_\text{c}(t) =\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right) &=\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right)*\delta(t-n T_c) \\
&=\sum_{n\in\mathbb{Z}}s_\text{a}[n]\delta(t-n T_c)* \text{rect}\left(\frac{t-nT_c}{\tau}\right)
\end{aligned}](/forum/latexrender/pictures/39433271ebdcf143caa82514597726f0.png)
se adesso si definiscono
![s_\text{ci}(t):=\sum_{n\in\mathbb{Z}}s_\text{a}[n]\delta(t-n T_c)=\text{camp. ideale } s_a(t) s_\text{ci}(t):=\sum_{n\in\mathbb{Z}}s_\text{a}[n]\delta(t-n T_c)=\text{camp. ideale } s_a(t)](/forum/latexrender/pictures/eac941d6de199cf29992a823bfd0cf64.png)

si conclude che lo spettro del segnale campionato ora è

avendo sfruttato il risultato trovato nel primo caso. Il risultato trovato mette in luce che il campionamento ZOH comporta delle distorsioni, in quanto, come si nota nell'ultima espressione, ogni replica è riscalata di un fattore

che varia frequenza per frequenza.
Facendo riferimento al solito esempio di spettro triangolare, adesso lo spettro del sengnale campionato assume la seguente forma
La distorsione risulta trascurabile quando il

è approssimativamente costante nella banda occupata da ogni singola replica.
Questo avviene per esempio nell'intorno della continua quando

(in tal caso il sinc si appiattisce tendendo all'unità) , e in questo modo si torna al caso di campionamento ideale (gli impulsi tendo a delle delta).
In sostanza, un buon campionamento ZOH dipende da due parametri: la durata degli impulsi che determinano la distorsione intrinseca del metodo di campionamento, e il tempo di campionamento che determina l'eventuale distorsione di aliasing.
Supponendo di non essere in grado di generare impulsi sufficientemente brevi, si può sempre rimediare alla distorsione considerando una opportuna equalizzazione post-campionamento che compensi la distorsione di campionamento
Una volta equalizzato il segnale campionato si può ricostruire con buona approssimazione il segnale di partenza andando a filtrare la replica in banda base, e riscalarla opportunamente.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)




 instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.

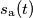
 , detto
, detto ![s[n]:=s_\text{a}(nT_c), \qquad n\in\mathbb{Z} s[n]:=s_\text{a}(nT_c), \qquad n\in\mathbb{Z}](/forum/latexrender/pictures/0a657f8c61fa7eb42b1e6c8d58cb2610.png)
 , utilizza pressoché sempre in analisi.
, utilizza pressoché sempre in analisi.
![\begin{aligned} s_c(t)&=\sum_{n\in\mathbb{Z}}s[n]\delta(t-nT_c) \\
&=\sum_{n\in\mathbb{Z}}s_a(t)\delta(t-nT_c)=s_a(t)\sum_{n\in\mathbb{Z}}\delta(t-nT_c) \end{aligned} \begin{aligned} s_c(t)&=\sum_{n\in\mathbb{Z}}s[n]\delta(t-nT_c) \\
&=\sum_{n\in\mathbb{Z}}s_a(t)\delta(t-nT_c)=s_a(t)\sum_{n\in\mathbb{Z}}\delta(t-nT_c) \end{aligned}](/forum/latexrender/pictures/580e02baabac30311b14262275152d6d.png)

 la trasformata di Fourier (ossia lo
la trasformata di Fourier (ossia lo  , si trova
, si trova
 indica il ben noto prodotto di convoluzione. Tra primo e secondo membro si è utilizzato il
indica il ben noto prodotto di convoluzione. Tra primo e secondo membro si è utilizzato il  , è, a meno del fattore di scala
, è, a meno del fattore di scala  , dato dalla sovrapposizione di infinite repliche
, dato dalla sovrapposizione di infinite repliche  ), tutte centrate in multipli della
), tutte centrate in multipli della  , cioè
, cioè

 , allora lo spettro del segnale campionato è il seguente:
, allora lo spettro del segnale campionato è il seguente:
 , sempre con cadenza regolare di periodo
, sempre con cadenza regolare di periodo  .
.
 .
.
 e allo stesso tempo di un fattore proprio
e allo stesso tempo di un fattore proprio  .
.
 .
.
![s_\text{c}(t)=\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right) s_\text{c}(t)=\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right)](/forum/latexrender/pictures/7f589de1135e50bd578a05b51fa11aaf.png)
![\begin{aligned}s_\text{c}(t) =\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right) &=\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right)*\delta(t-n T_c) \\
&=\sum_{n\in\mathbb{Z}}s_\text{a}[n]\delta(t-n T_c)* \text{rect}\left(\frac{t-nT_c}{\tau}\right)
\end{aligned} \begin{aligned}s_\text{c}(t) =\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right) &=\sum_{n\in\mathbb{Z}}s_\text{a}[n] \, \text{rect}\left(\frac{t-nT_c}{\tau}\right)*\delta(t-n T_c) \\
&=\sum_{n\in\mathbb{Z}}s_\text{a}[n]\delta(t-n T_c)* \text{rect}\left(\frac{t-nT_c}{\tau}\right)
\end{aligned}](/forum/latexrender/pictures/39433271ebdcf143caa82514597726f0.png)
![s_\text{ci}(t):=\sum_{n\in\mathbb{Z}}s_\text{a}[n]\delta(t-n T_c)=\text{camp. ideale } s_a(t) s_\text{ci}(t):=\sum_{n\in\mathbb{Z}}s_\text{a}[n]\delta(t-n T_c)=\text{camp. ideale } s_a(t)](/forum/latexrender/pictures/eac941d6de199cf29992a823bfd0cf64.png)


 che varia frequenza per frequenza.
che varia frequenza per frequenza.
 (in tal caso il sinc si appiattisce tendendo all'unità) , e in questo modo si torna al caso di campionamento ideale (gli impulsi tendo a delle delta).
(in tal caso il sinc si appiattisce tendendo all'unità) , e in questo modo si torna al caso di campionamento ideale (gli impulsi tendo a delle delta).

