Problema 1:

Partiamo da quello e andiamo avanti

Dopo che abbiamo capito come risolverlo in un modo (che sarà quello proposto stesso da te) vediamo anche in quanti altri modi si può vedere la faccenda :)
Moderatori: ![]() PietroBaima,
PietroBaima, ![]() Ianero
Ianero


Ianero ha scritto:Problema 1:Piercarlo ti dispiacerebbe raccogliere in un'unica risposta qui sotto il tuo tentativo di soluzione?
Partiamo da quello e andiamo avanti
 reale avrebbe dovuto farmi drizzare le antenne, io comunque sono partito dalle mie uniche e ormai arrugginite conoscenze di trigonometria che ho acquisito sotto insegnante una quarantina di anni fa e che ho visto fin da allora come un'estensione del teorema di Pitagora, indipendentemente dalla correttezza o meno di questo approccio che comunque, per le mie (modeste) esigenze mi è sempre andato più che bene.
reale avrebbe dovuto farmi drizzare le antenne, io comunque sono partito dalle mie uniche e ormai arrugginite conoscenze di trigonometria che ho acquisito sotto insegnante una quarantina di anni fa e che ho visto fin da allora come un'estensione del teorema di Pitagora, indipendentemente dalla correttezza o meno di questo approccio che comunque, per le mie (modeste) esigenze mi è sempre andato più che bene. , toglierndo o aggiungendo
, toglierndo o aggiungendo  "
" appunto. In un in singolo cerchio di 360° esistono solo quattro angoli che soddisfano la richiesta +/- 45° e +/- 135°, corrispondenti a
appunto. In un in singolo cerchio di 360° esistono solo quattro angoli che soddisfano la richiesta +/- 45° e +/- 135°, corrispondenti a  ,
, 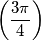 ,
,  e
e  .
.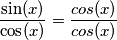 per "ravvivare" la domanda a cui poi
per "ravvivare" la domanda a cui poi Facciamo un grafico della funzione seno e della funzione coseno.
Cosa ti dice il grafico?
PS. per coloro che tutte le volte che posto un qualcosa fatto in mathematica mi chiedono il codice, eccolo qui:
- Codice: Seleziona tutto
Plot[
{Sin[x], Cos[x]},
{x, -2 \[Pi], 2 \[Pi]}, Prolog ->
{Red,
PointSize[0.02],
Point[{{\[Pi]/4, 1/Sqrt[2]}, {\[Pi]/4 + \[Pi], -1/Sqrt[2]
}
}
]
}
]
Beh, i due puntini marcano il montante di salita della sinusoide positiva:
+45°
e negativa;
+225°
Questo forse è da scrivere così:
-45°
E poi? Le soluzioni con numeri reali sono solo queste? E dillo, no?
(c'entra qualcosa l'uso di considerare
come parte immaginaria e
come parte reale di un numero complesso? Se è così devo ripescare come funzionano i segni a seconda che le componenti di un numero complesso siano di segno concorde o discorde tra loro).
Dal grafico non hai modo di saperlo con certezza. Puoi solo fare delle ipotesi.
Dal cerchio trigonometrico va meglio, ma hai trovato soluzioni diverse...
Come la mettiamo?
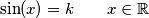

La risposta viene da un ragionamento sulla geometria del cerchio, avendo in mente Pitagora: se la condizione da soddisfare è che seno e coseno abbiano lo stesso valore allora, risalendo al teorema di Pitagora, si deve cercare quella situazione in cui i due cateti sono uguali e questa corrisponde ad un triangolo rettangolo ottenuto dal sezionamento di un quadrato lungo una delle due diagonali.
 e
e  , a parte i cambiamenti di segno e di verso, si ripetono ogni 90 gradi. Quindi cosa c'è che non va? Spiegatemi!
, a parte i cambiamenti di segno e di verso, si ripetono ogni 90 gradi. Quindi cosa c'è che non va? Spiegatemi!![[sen(x)/cos(x)]=1 [sen(x)/cos(x)]=1](/forum/latexrender/pictures/9deed77a300af3e8b7d35352a0d25659.png) quindi tg(x)=1 di conseguenza x=45°+k180
quindi tg(x)=1 di conseguenza x=45°+k180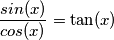
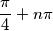 con
con  intero grande a piacere o scritto
intero grande a piacere o scritto 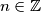 .
.Visitano il forum: Nessuno e 4 ospiti