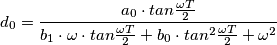assegnate delle specifiche relative ad un filtro passa basso di Butterworth, sto cercando di ricavare il corrispondente filtro digitale.
Assegnate le specifiche, ricavo la seguente funzione di trasferimento, che posso confermare sia con Matlab sia con la "classica" analisi di Darlinghton.
La funzione di trasferimento è la seguente:

A cui corrisponde un ordine del filtro
 e una frequenza di taglio
e una frequenza di taglio  .
.Come scritto sopra, ho verificato che la FDT nel dominio di s fosse quella che ho scritto sopra, sia analiticamente (ricavo selettività e fattore di discriminazione, ordine del filtro, sintesi di Darlinghton etc...) e sia con il calcolatore (tramite semplici funzioni di Matlab).
Definito questo, e definita la frequenza di campionamento
 ,ricavo con MATLAB la corrispondente FDT in z, che risulta del tipo:
,ricavo con MATLAB la corrispondente FDT in z, che risulta del tipo:
dove
 sono dei coefficienti che mi ricavo con Matlab tramite semplici funzioni e passaggi.
sono dei coefficienti che mi ricavo con Matlab tramite semplici funzioni e passaggi.Ora, il procedimento per passare da
 a
a  è quello di sostituire con la seguente relazione giusto?
è quello di sostituire con la seguente relazione giusto?
Definito ciò, qualora dovessi fare le cose analiticamente (e non tramite Matlab) esistono delle formule "più dirette" che mi permettono di sostituire i valori dei coefficienti
 senza dover sostituire la relazione di sopra ??
senza dover sostituire la relazione di sopra ??Magari per filtri di ordine 2 e/o 3.
Grazie in anticipo a tutti quanti

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)

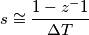


 :
: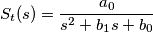
 del tipo seguente:
del tipo seguente:


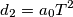
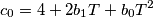
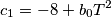
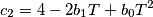


 hai usato?
hai usato?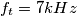 ed un ordine pari a
ed un ordine pari a 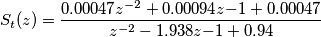

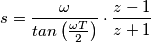
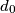 :
: