CASO 1:
![M=\left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1 \end{matrix}\right] M=\left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1 \end{matrix}\right]](/forum/latexrender/pictures/df9a708d5e3054aa7220c19b40ee8537.png)
![R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right] R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]](/forum/latexrender/pictures/cdcce3fbbc6b94951eef7f631dbe8653.png)
![\bar{R}=M\cdot R\cdot M^T=\left[\begin{matrix} 16 & -8 \\ -8 & 15\end{matrix}\right] \bar{R}=M\cdot R\cdot M^T=\left[\begin{matrix} 16 & -8 \\ -8 & 15\end{matrix}\right]](/forum/latexrender/pictures/f5c0053b2cb7baaf638ace4c88f7f2e5.png)
![E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\40 \\-20 \end{matrix}\right] E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\40 \\-20 \end{matrix}\right]](/forum/latexrender/pictures/a324e742e91df3c422bf43271db58a72.png)
![\bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 40 \\20 \end{matrix}\right] \bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 40 \\20 \end{matrix}\right]](/forum/latexrender/pictures/87d69dddd6cea1b7a9698d12935bb8f5.png)
![\bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 4,31 & 3,63\end{matrix}\right] \bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 4,31 & 3,63\end{matrix}\right]](/forum/latexrender/pictures/22f66abdd908dcdb6fc86d51ba6b204a.png)
![I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 4,31 & -0,68 & -4,31 & 3,63 & -3,63 & 4,31 & -3,63\end{matrix}\right] I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 4,31 & -0,68 & -4,31 & 3,63 & -3,63 & 4,31 & -3,63\end{matrix}\right]](/forum/latexrender/pictures/530fce802cd3767a7dad749c36bc64ee.png)
Per Rth ho fatto così:

Per Vth non sono sicuro:







CASO 2:



![R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 32 & 0 & 0 & 0 & 0 & 0\end{matrix}\right] R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 32 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]](/forum/latexrender/pictures/3dd13608bb0eb01984cc6799b56ebc1c.png)
![\bar{R}=M\cdot R\cdot M^T=\left[\begin{matrix} 16 & -8 \\ 24 & -17\end{matrix}\right] \bar{R}=M\cdot R\cdot M^T=\left[\begin{matrix} 16 & -8 \\ 24 & -17\end{matrix}\right]](/forum/latexrender/pictures/767f484f156c2b6ffc9cf9f1cf13324b.png)
![E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\40 \end{matrix}\right] E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\40 \end{matrix}\right]](/forum/latexrender/pictures/9555402be88d3a32ade600b22ac1f298.png)
![\bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 0 \\ -40 \end{matrix}\right] \bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 0 \\ -40 \end{matrix}\right]](/forum/latexrender/pictures/b18207c795bbc6bc69d5b26eb42405ca.png)
![\bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 4 & 8\end{matrix}\right] \bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 4 & 8\end{matrix}\right]](/forum/latexrender/pictures/01c2b9502e29bc1b5d296c888c545165.png)
![I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 4 & 4 & -4 & 8 & -8 & 4 & -8\end{matrix}\right] I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 4 & 4 & -4 & 8 & -8 & 4 & -8\end{matrix}\right]](/forum/latexrender/pictures/5d19033885ca80f8fbdaad037c04f01f.png)
Grazie.
Moderatori: ![]() g.schgor,
g.schgor, ![]() IsidoroKZ
IsidoroKZ
![M=\left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1 \end{matrix}\right] M=\left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1 \end{matrix}\right]](/forum/latexrender/pictures/df9a708d5e3054aa7220c19b40ee8537.png)
![R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right] R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]](/forum/latexrender/pictures/cdcce3fbbc6b94951eef7f631dbe8653.png)
![\bar{R}=M\cdot R\cdot M^T=\left[\begin{matrix} 16 & -8 \\ -8 & 15\end{matrix}\right] \bar{R}=M\cdot R\cdot M^T=\left[\begin{matrix} 16 & -8 \\ -8 & 15\end{matrix}\right]](/forum/latexrender/pictures/f5c0053b2cb7baaf638ace4c88f7f2e5.png)
![E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\40 \\-20 \end{matrix}\right] E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\40 \\-20 \end{matrix}\right]](/forum/latexrender/pictures/a324e742e91df3c422bf43271db58a72.png)
![\bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 40 \\20 \end{matrix}\right] \bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 40 \\20 \end{matrix}\right]](/forum/latexrender/pictures/87d69dddd6cea1b7a9698d12935bb8f5.png)
![\bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 4,31 & 3,63\end{matrix}\right] \bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 4,31 & 3,63\end{matrix}\right]](/forum/latexrender/pictures/22f66abdd908dcdb6fc86d51ba6b204a.png)
![I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 4,31 & -0,68 & -4,31 & 3,63 & -3,63 & 4,31 & -3,63\end{matrix}\right] I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 4,31 & -0,68 & -4,31 & 3,63 & -3,63 & 4,31 & -3,63\end{matrix}\right]](/forum/latexrender/pictures/530fce802cd3767a7dad749c36bc64ee.png)











![R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 32 & 0 & 0 & 0 & 0 & 0\end{matrix}\right] R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 32 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]](/forum/latexrender/pictures/3dd13608bb0eb01984cc6799b56ebc1c.png)
![\bar{R}=M\cdot R\cdot M^T=\left[\begin{matrix} 16 & -8 \\ 24 & -17\end{matrix}\right] \bar{R}=M\cdot R\cdot M^T=\left[\begin{matrix} 16 & -8 \\ 24 & -17\end{matrix}\right]](/forum/latexrender/pictures/767f484f156c2b6ffc9cf9f1cf13324b.png)
![E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\40 \end{matrix}\right] E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\40 \end{matrix}\right]](/forum/latexrender/pictures/9555402be88d3a32ade600b22ac1f298.png)
![\bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 0 \\ -40 \end{matrix}\right] \bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 0 \\ -40 \end{matrix}\right]](/forum/latexrender/pictures/b18207c795bbc6bc69d5b26eb42405ca.png)
![\bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 4 & 8\end{matrix}\right] \bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 4 & 8\end{matrix}\right]](/forum/latexrender/pictures/01c2b9502e29bc1b5d296c888c545165.png)
![I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 4 & 4 & -4 & 8 & -8 & 4 & -8\end{matrix}\right] I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 4 & 4 & -4 & 8 & -8 & 4 & -8\end{matrix}\right]](/forum/latexrender/pictures/5d19033885ca80f8fbdaad037c04f01f.png)

EdmondDantes ha scritto:Ormai le regole del forum le conosci.
3) D: Come mai inizi con la pseudo soluzione e inserisci il testo del problema alla fine?
R: Non lo so, ho pensato di fare cosi'...
D: Non ci siamo!
 . Il motivo è che non ho capito come mettere l'immagine all'inizio del post.
. Il motivo è che non ho capito come mettere l'immagine all'inizio del post.EdmondDantes ha scritto: D: Ho dato una lettura veloce al tuo messaggio, saltando tutti i papiri matriciali e l'occhio si e' fermato sul circuito base per il calcolo della Rth del caso 1. Mi hai quasi accecato. Mi vuoi male?
R: Ma perche' dici questo? Ho spento tutti i generatori. Che ho fatto?
D: Cosa non hai fatto, vorrai dire! Non hai studiato! Inutile scrivere m2 di matrici e poi sbagli i concetti base. Vai a studiare.

![M=\left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1 \end{matrix}\right] M=\left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1 \end{matrix}\right]](/forum/latexrender/pictures/df9a708d5e3054aa7220c19b40ee8537.png)
![R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right] R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]](/forum/latexrender/pictures/cdcce3fbbc6b94951eef7f631dbe8653.png)
![\bar{R}=M\cdot R\cdot M^T= \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]\left[\begin{matrix} 1 & 0 \\ -1 & 1 \\ -1 & 0 \\ 0 & 1 \\ 0 & -1 \\ 1 & 0 \\ 0 & -1\end{matrix}\right]= \bar{R}=M\cdot R\cdot M^T= \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]\left[\begin{matrix} 1 & 0 \\ -1 & 1 \\ -1 & 0 \\ 0 & 1 \\ 0 & -1 \\ 1 & 0 \\ 0 & -1\end{matrix}\right]=](/forum/latexrender/pictures/3d8fe56c5bfbcaf31d4b001c87440578.png)
![=\left[\begin{matrix} 16 & -8 \\ -8 & 15\end{matrix}\right] =\left[\begin{matrix} 16 & -8 \\ -8 & 15\end{matrix}\right]](/forum/latexrender/pictures/768767c77807903490c0854e59bb93b6.png)
![E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\40 \\-20 \end{matrix}\right] E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\40 \\-20 \end{matrix}\right]](/forum/latexrender/pictures/a324e742e91df3c422bf43271db58a72.png)
![\bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\0 \end{matrix}\right]- \bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\0 \end{matrix}\right]-](/forum/latexrender/pictures/f6aa4e0b1a8e143a278e19f6211a69ee.png)
![- \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\40 \\-20 \end{matrix}\right] = \left[\begin{matrix} 40 \\20 \end{matrix}\right] - \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\40 \\-20 \end{matrix}\right] = \left[\begin{matrix} 40 \\20 \end{matrix}\right]](/forum/latexrender/pictures/b2faaa9c36da0d7d68ae05c0568ed9db.png)
![\bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 0,085 & 0,045 \\ 0,045 & 0,090\end{matrix}\right]\left[\begin{matrix} 40 \\20 \end{matrix}\right] =\left[\begin{matrix} 4,31 & 3,63\end{matrix}\right] \bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 0,085 & 0,045 \\ 0,045 & 0,090\end{matrix}\right]\left[\begin{matrix} 40 \\20 \end{matrix}\right] =\left[\begin{matrix} 4,31 & 3,63\end{matrix}\right]](/forum/latexrender/pictures/ecc0f683dd728f652a43a3cd602eef16.png)
![I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 4,31 & 3,63\end{matrix}\right] = I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 4,31 & 3,63\end{matrix}\right] =](/forum/latexrender/pictures/2216ccc9f7b01d43d86a6a939dc6be6f.png)
![=\left[\begin{matrix} 4,31 & -0,68 & -4,31 & 3,63 & -3,63 & 4,31 & -3,63\end{matrix}\right] =\left[\begin{matrix} 4,31 & -0,68 & -4,31 & 3,63 & -3,63 & 4,31 & -3,63\end{matrix}\right]](/forum/latexrender/pictures/bacbe9d2338f4b2e6d1234d09a0b6156.png)
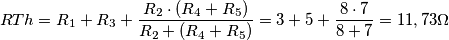


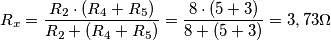
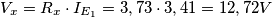
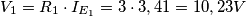

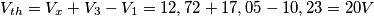

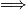
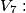 tensione del lato del gen. comandato
tensione del lato del gen. comandato
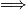
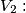 legge di ohm lato che comanda
legge di ohm lato che comanda
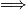
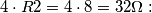 resistenza da inserire nella matrice delle
resistenza da inserire nella matrice delle 
![R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 32 & 0 & 0 & 0 & 0 & 0\end{matrix}\right] R=\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 32 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]](/forum/latexrender/pictures/3dd13608bb0eb01984cc6799b56ebc1c.png)
![\bar{R}=M\cdot R\cdot M^T= \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 32 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]\left[\begin{matrix} 1 & 0 \\ -1 & 1 \\ -1 & 0 \\ 0 & 1 \\ 0 & -1 \\ 1 & 0 \\ 0 & -1\end{matrix}\right]= \bar{R}=M\cdot R\cdot M^T= \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 32 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]\left[\begin{matrix} 1 & 0 \\ -1 & 1 \\ -1 & 0 \\ 0 & 1 \\ 0 & -1 \\ 1 & 0 \\ 0 & -1\end{matrix}\right]=](/forum/latexrender/pictures/12ed5c50a4f92d558e79e9583b0606a0.png)
![=\left[\begin{matrix} 16 & -8 \\ 24 & -17\end{matrix}\right] =\left[\begin{matrix} 16 & -8 \\ 24 & -17\end{matrix}\right]](/forum/latexrender/pictures/fd8a3cec2436e1ace392a66049961a7e.png)
![E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\40 \end{matrix}\right] E=\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\40 \end{matrix}\right]](/forum/latexrender/pictures/9555402be88d3a32ade600b22ac1f298.png)
![\bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 32 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\0 \end{matrix}\right]- \bar{V}=M\cdot R\cdot A - M\cdot E= \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 32 & 0 & 0 & 0 & 0 & 0\end{matrix}\right]\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\0 \end{matrix}\right]-](/forum/latexrender/pictures/a55de6906afa2de2738e4831fe1e400b.png)
![- \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\40 \end{matrix}\right] =\left[\begin{matrix} 40 \\ 0 \end{matrix}\right] - \left[\begin{matrix} 1 & -1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & -1\end{matrix}\right]\left[\begin{matrix} 0 \\ 0 \\0 \\0 \\0 \\0 \\40 \end{matrix}\right] =\left[\begin{matrix} 40 \\ 0 \end{matrix}\right]](/forum/latexrender/pictures/f1f816ab7a92d841d3adc055aefd2d5c.png)
![\bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 0,212 & -0,1 \\ 0,3 & -0,2\end{matrix}\right]\left[\begin{matrix} 40 \\ 0 \end{matrix}\right] = \left[\begin{matrix} 8,5 & 12\end{matrix}\right] \bar{I}^{ T}=\bar{R}^{-1}\cdot \bar{V}= \left[\begin{matrix} 0,212 & -0,1 \\ 0,3 & -0,2\end{matrix}\right]\left[\begin{matrix} 40 \\ 0 \end{matrix}\right] = \left[\begin{matrix} 8,5 & 12\end{matrix}\right]](/forum/latexrender/pictures/61c7e3a355a18cc90a78f022c46843de.png)
![I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 1 & 0 \\ -1 & 1 \\ -1 & 0 \\ 0 & 1 \\ 0 & -1 \\ 1 & 0 \\ 0 & -1\end{matrix}\right]\left[\begin{matrix} 8,5 \\ 12\end{matrix}\right] =\left[\begin{matrix} 8,5 & 3,5 & -8,5 & 12 & -12 & 8,5 & -12\end{matrix}\right] I=M^{ T}\cdot \bar{I} = \left[\begin{matrix} 1 & 0 \\ -1 & 1 \\ -1 & 0 \\ 0 & 1 \\ 0 & -1 \\ 1 & 0 \\ 0 & -1\end{matrix}\right]\left[\begin{matrix} 8,5 \\ 12\end{matrix}\right] =\left[\begin{matrix} 8,5 & 3,5 & -8,5 & 12 & -12 & 8,5 & -12\end{matrix}\right]](/forum/latexrender/pictures/85c2bfdbb733b4d3cdda89b818be8cbc.png)
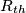 il risultato era giusto. Nel riportare i conti non ho scritto la somma con
il risultato era giusto. Nel riportare i conti non ho scritto la somma con  ed
ed 
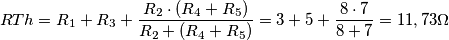



Torna a Elettrotecnica generale
Visitano il forum: Nessuno e 32 ospiti