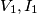 che considero sono l'ingresso dello stub quindi quello che entra prima del ramo parallelo a corto circuito (e perciò tengo conto delle correnti al nodo) mentre l'uscita
che considero sono l'ingresso dello stub quindi quello che entra prima del ramo parallelo a corto circuito (e perciò tengo conto delle correnti al nodo) mentre l'uscita 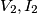 è la tensione sul carico, dopo tutta la distanza
è la tensione sul carico, dopo tutta la distanza  . Ora la cosa strana che mi viene fuori è che rispetto a una qualsiasi linea con impedenza caratteristica di lunghezza L, qui l'aggiunta dello stub in ingresso va a cambiare il solo parametro C mentre gli altri rimangono identici. Secondo vuoi può essere così circa? (quella strana con la tangente è l'impedenza introdotta dallo stub che ha una lunghezza
. Ora la cosa strana che mi viene fuori è che rispetto a una qualsiasi linea con impedenza caratteristica di lunghezza L, qui l'aggiunta dello stub in ingresso va a cambiare il solo parametro C mentre gli altri rimangono identici. Secondo vuoi può essere così circa? (quella strana con la tangente è l'impedenza introdotta dallo stub che ha una lunghezza 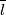 mentre
mentre  è l'impedenza di carico).
è l'impedenza di carico). 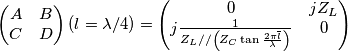
Per passaggi più dettagliati provo a scrivervi domani se ho tempo, spero riusciate a vedere anche così a occhio se qualcosa non torna. Questa matrice mi sarà utile successivamente per fare cose più complesse.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)


 .
.
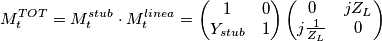





 e lungo
e lungo  , senza perdite
, senza perdite


 altro non è che
altro non è che essendo, in questa equazionoe,
essendo, in questa equazionoe,  poiché lo stub è chiuso.
poiché lo stub è chiuso.


 all'interno del sistema di equazioni:
all'interno del sistema di equazioni:


