Ti do un consiglio preliminare per cercare di aiutarti nell'affrontare questo tipo di problemi e per risolvere anche i dubbi annessi.
Il sistema di riferimento, quando si risolve un problema di fisica, si fissa prima di cominciare.
Non l'hai fatto in [1], per cui per non allungare troppo il brodo facciamo che te lo fisso io, così:
Fatto ciò, ti dico inoltre che in questi problemi i vettori non sono applicati in nessun punto. La trattazione matematica che si utilizza solitamente per risolverli prevede l'uso di vettori liberi, per i quali è sufficiente specificare solo modulo, direzione e verso. Di conseguenza frasi come questa:
ziomangrovia ha scritto:Il momento angolare ... dal cerchio verso il punto P.
non sono proprio il massimo.
Veniamo al tuo dubbio.
Il vettore (libero) che descrive la forza di gravità cui è soggetta la pallina attaccata al filo è, nel particolare sistema di riferimento che abbiamo scelto, questo:
Il calcolo del momento meccanico si basa sulla conoscenza di un polo, che fissiamo ad esempio nel punto in cima in cui si è bloccato il filo, e sulla conoscenza di un altro vettore: il braccio.
Disegniamoli:
Come saprai, il calcolo del momento angolare rispetto al polo scelto, si ottiene mediante la seguente:

che in notazione vettoriale diventa, nel nostro sistema di riferimento:


dove ho indicato con

il raggio dell'orbita della pallina, con

l'angolo tra

(vettore posizione della pallina) e

, con

la lunghezza del filo e con

l'angolo tra il filo e l'asse (a sua volta parallelo a

).
Di conseguenza:

dove si vede molto bene come mai sia assente una componente di momento meccanico parallela all'asse.
Come ti dicevo (*) in [4] e [6], questa proprietà è generale, vale sempre che il prodotto vettoriale tra un vettore qualsiasi

e uno della forma

non presenta mai una componente parallela a

, infatti è sufficiente rifare lo stesso calcolo che ho fatto sopra con:

(*) nei messaggi [4] e [6] ho indicato i vettori con una sottolineatura, in questo messaggio li ho indicati in grassetto.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



 è perpendicolare sia al vettore
è perpendicolare sia al vettore 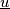 che a
che a  .
.
 il prodotto vettoriale di tale vettore con qualsiasi altro non potrà avere componente non nulla lungo quell'asse.
il prodotto vettoriale di tale vettore con qualsiasi altro non potrà avere componente non nulla lungo quell'asse.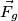 combinato con qualsiasi altro vettore posizione
combinato con qualsiasi altro vettore posizione  (che è il raggio della circonferenza) mi individua un certo piano che supponiamo sia
(che è il raggio della circonferenza) mi individua un certo piano che supponiamo sia 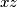 quindi il loro prodotto (momento meccanico
quindi il loro prodotto (momento meccanico 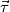 ) sarà un vettore
) sarà un vettore 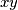 .
.  ed il vettore
ed il vettore 






 il raggio dell'orbita della pallina, con
il raggio dell'orbita della pallina, con  l'angolo tra
l'angolo tra  (vettore posizione della pallina) e
(vettore posizione della pallina) e  , con
, con  la lunghezza del filo e con
la lunghezza del filo e con  l'angolo tra il filo e l'asse (a sua volta parallelo a
l'angolo tra il filo e l'asse (a sua volta parallelo a  ).
).
 e uno della forma
e uno della forma  non presenta mai una componente parallela a
non presenta mai una componente parallela a 