Utilizzando
Geogebra è possibile disegnare e fare i calcoli geometrici necessari. Geogebra non permette di calcolare l'area che ci interessa, viene calcolata come differenza tra l'area del settore circolare e il triangolo. Allego il file di Geogebra, i punti modificabili sono A e B, tutti gli altri dati sono poi aggiornati automaticamente.
Utilizzando come CAS (Computer Algebra System)
Maxima e il suo front-end
wxMaxima è possibile fare tutti i calcoli necessari per trovare una soluzione approssimata di

e poi verificarla con i valori di Geogebra.
Area del settore circolare:
- Codice: Seleziona tutto
AC: (R^2 * theta) / 2;

Lunghezza corda:
- Codice: Seleziona tutto
c: R * sin(theta / 2) * 2;

Altezza triangolo:
- Codice: Seleziona tutto
d: R * cos(theta / 2);

Area triangolo:
- Codice: Seleziona tutto
AT: trigreduce(c * d / 2);

Area segmento circolare:
- Codice: Seleziona tutto
A: factor(AC - AT);

Se tentiamo di risolvere l'equazione rispetto a

Maxima non trova nessuna soluzione valida.
Utilizziamo l'approssimazione di Taylor di

fino al 3 grado:
- Codice: Seleziona tutto
T3: taylor(sin(theta), theta, 0, 3);

Utilizzando l'approssimazione di Taylor troviamo 3 soluzioni, 2 complesse e una reale, prendiamo quest'ultima:
- Codice: Seleziona tutto
solve(ev(A, sin(theta) = T3) = 'A, theta)$
s:rootscontract(xthru(rhs(%[3])));

Con la soluzione approssimata possiamo calcolare l'altezza approssimata:
- Codice: Seleziona tutto
h:rootscontract(ratsimp(ev(R - d, theta=s)));

Sostituiamo i valori di Geogebra
- Codice: Seleziona tutto
ev(h, R=3.81, A=2.17), float;

Troviamo un valore di

vicino al valore

di Geogebra. Maggiore è l'angolo

maggiore è l'errore che si commette con all'approssimazione di Taylor.
Possiamo utilizzare il metodo delle tangenti (Newton-Raphson) per trovare, se possibile, una migliore soluzione numerica:
https://it.wikipedia.org/wiki/Metodo_delle_tangentiPuliamo tutta la memoria di Maxima, carichiamo il modulo con il codice per il metodo di Newton e impostiamo i dati numerici di partenza:
- Codice: Seleziona tutto
kill(all)$
load ("newton1")$
dati:[R=3.81, A=2.17];
Per trovare la soluzione bisogna impostare un punto iniziale

e una tolleranza

:
- Codice: Seleziona tutto
sol: newton(ev((R^2*(theta - sin(theta)))/2 - A, dati), theta, 0.1, 1E-4)$
float(sol * 180 / %pi);
ev(R - R * cos(theta / 2), dati, theta=sol);


L'angolo

in gradi sessadecimale e l'altezza

sono molto vicini ai valori di Geogebra quindi si tratta di una soluzione migliore.


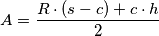 ma alla fine è riconducibile sempre alla precedente.
ma alla fine è riconducibile sempre alla precedente.
 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



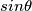 a
a 



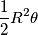 . L'area del
. L'area del 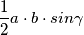 , che nel nostro caso
, che nel nostro caso 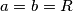 e
e 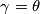 quindi
quindi 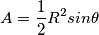 .
.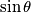 .
.

 e poi verificarla con i valori di Geogebra.
e poi verificarla con i valori di Geogebra.




 fino al 3 grado:
fino al 3 grado:



 di Geogebra. Maggiore è l'angolo
di Geogebra. Maggiore è l'angolo  e una tolleranza
e una tolleranza  :
:

