Ho il seguente esercizio.
Il segnale Vout(t) in uscita ad un certo sistema elettronico è la risultante di più componenti armoniche come di seguito rappresentate:

dove:
![V_{k}=\frac{12}{k}10^{-3}[V] V_{k}=\frac{12}{k}10^{-3}[V]](/forum/latexrender/pictures/4751d87d76f4e5f87be60285a92b2599.png)
e
![\omega _{k}=8\cdot k^{3}\cdot 10^{3}[rad/s] \omega _{k}=8\cdot k^{3}\cdot 10^{3}[rad/s]](/forum/latexrender/pictures/9e5fc62ae19b7be0482c1a05764b9325.png)
Si determini l’ordine del filtro da utilizzare in modo da garantire un guadagno alla frequenza della prima armonica pari a 18 dB e non superiore a -5 dB per la seconda armonica. Si progetti quindi il sistema filtrante giustificando le scelte effettuate.
(tratto dall’esame di Stato di Elettrotecnica ed Elettronica, articolazione Elettronica, del 2016)
La soluzione non mi sembra impossibile. Però, ho un paio di dubbi che volevo qui mostrare.
Allora, l’espressione analitica della tensione d’uscita, secondo quanto riportato dalla traccia, risulta:
![V_{out}(t)=12\cdot sin(8\cdot 10^{3}t)+6\cdot sin(64\cdot 10^{3}t)+4\cdot sin(216\cdot 10^{3}t)+3\cdot sin(2048\cdot 10^{3}t) [mV] V_{out}(t)=12\cdot sin(8\cdot 10^{3}t)+6\cdot sin(64\cdot 10^{3}t)+4\cdot sin(216\cdot 10^{3}t)+3\cdot sin(2048\cdot 10^{3}t) [mV]](/forum/latexrender/pictures/0a487ff3a7de85afcf9dad1bda94f959.png)
Le frequenze delle prime due armoniche valgono:
![f_{1}=\frac{\omega _{1}}{2\pi }=1273[Hz] f_{1}=\frac{\omega _{1}}{2\pi }=1273[Hz]](/forum/latexrender/pictures/ef87696f3786c5e82ce0d9bb5e1a477b.png)
e
![f_{2}=\frac{\omega _{2}}{2\pi }=10.186[Hz] f_{2}=\frac{\omega _{2}}{2\pi }=10.186[Hz]](/forum/latexrender/pictures/ff5d131e0867b6595937f80f36128846.png)
Ora determino la pendenza minima richiesta da un filtro (evidentemente) passa-basso.

E qui ho il primo dubbio e riguarda l'unità di misura di pmin: mi verrebbe da dire dB e non dB/Hz. perché? perché in fisica l'argomento di una funzione trascendente (come il logaritmo) deve essere sempre un numero puro. E lo è anche il risultato della funzione stessa. E' corretto? Oppure è una boiata (scusate il francesismo)? E, se fosse corretto, che significato avrebbe pmin? Non certo quello di una pendenza, semmai quello dell'escursione, in dB, compiuta dal guadagno in quell'intervallo di frequenza.
Ed ora vengo al secondo dubbio.
E' evidente che un filtro del primo ordine non risponde in modo adeguato alla richiesta della traccia. Ciò in quanto in un intervallo inferiore ad una decade si ha una diminuzione del guadagno superiore, in valore assoluto, a 20 dB.
La domanda, allora, è: un filtro del secondo ordine, sarà sufficiente? Ovvero, una pendenza di -40 dB/decade, risponderà a quanto richiesto dal tema? Se devo rispondere "ad occhio" direi di si! Ma come diceva un vecchio amico, occorre sempre fare il calcolo. E allora, come calcolo l'escursione del guadagno in una decade? Diciamo da 1273 Hz a 12730 Hz? Ecco, questo è il mio secondo dubbio.
Ho pensato a qualcosa ma, credo, non abbia la giusta decenza per essere proposto (in sostanza ho timore di "impicciarmi" con qualche "inghippo" legato alla natura logaritmica dell'asse delle frequenze).
Grazie per la pazienza.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)




 ; dobbiamo capire il messaggio che si vuole trasmettere.
; dobbiamo capire il messaggio che si vuole trasmettere.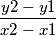
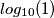 =0,
=0, 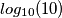 =1, differenza 1
=1, differenza 1 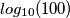 =2, differenza 2
=2, differenza 2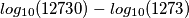
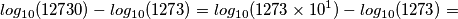
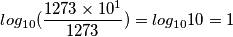

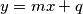
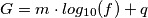
 .
. . Ma questo, operativamente, non mi aiuta molto!
. Ma questo, operativamente, non mi aiuta molto!
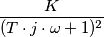
 e
e 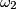 :
:

