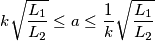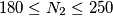vorrei un aiuto per la risoluzione del seguente esercizio.
Su due bobine mutuamente accoppiate sono state svolte le seguenti prove:
tenendo aperta la seconda bobina e facendo aumentare linearmente la corrente nella prima da zero a 10 A in 0,1 s, sono state misurate le tensioni E1=10 V e E2=6V;
tenendo aperta la prima bobina e facendo aumentare linearmente la corrente nella seconda da zero a 10 A in 0,1 s, sono state misurate le tensioni E1=6 V e E2=5V.
Calcolare: le induttanze delle due bobine; il coefficiente di mutua induzione; il fattore di accoppiamento; il numero di spire della seconda bobina, sapendo che N1=300 spire.
L'induttanza della prima bobina me la calcolo mettendo in relazione la tensione autoindotta con la variazione di corrente nella medesima bobina. Ovvero:

Il coefficiente di mutua induzione, invece, me lo calcolo mettendo in relazione la tensione mutuamente indotta nella seconda bobina con la variazione di corrente circolante nella prima bobina. Ovvero:

L'induttanza della seconda bobina me la calcolo mettendo in relazione la tensione autoindotta con la variazione di corrente nella medesima bobina. Ovvero:

Il fattore di accoppiamento, note L1, L2 ed M, lo calcolo con la relazione:

Ho difficoltà, invece, con il calcolo delle spire della seconda bobina.
Qualcuno può aiutarmi?
Grazie.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



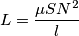
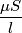 conoscendo
conoscendo  e
e  , infatti la formula di prima si può scrivere come:
, infatti la formula di prima si può scrivere come: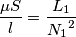
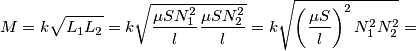
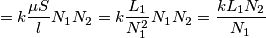
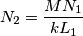

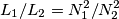
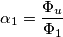
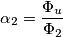
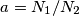 , e quindi di
, e quindi di 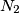 , che avrà come estremi i valori associati ai due casi particolari di
, che avrà come estremi i valori associati ai due casi particolari di  e
e 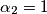 , ovvero
, ovvero