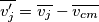Quello che volevo arrivare a concludere è che:

Dove:
 momento angolare totale del sistema materiale rispetto al polo O
momento angolare totale del sistema materiale rispetto al polo O momento angolare ("assoluto") del centro di massa rispetto ad O
momento angolare ("assoluto") del centro di massa rispetto ad O momento angolare ("relativo") del j-esimo punto materiale rispetto al centro di massa
momento angolare ("relativo") del j-esimo punto materiale rispetto al centro di massa momento angolare ("assoluto") del j-esimo punto materiale rispetto al polo O
momento angolare ("assoluto") del j-esimo punto materiale rispetto al polo Oovvero che il postulato del 1°teorema di Koenig (il momento angolare totale di un sistema è dato dalla somma del momento angolare assoluto del centro di massa e dalla somma dei momenti angolari relativi rispetto al centro di massa) equivale a fare la somma di tutti i momenti angolari assoluti
Il generico momento angolare (o momento della quantità di moto) viene calcolato come prodotto vettoriale tra posizione e prodotto di massa per velocità:
 dove s è lo spostamento, m è la massa e v la velocità; la formula precedente diventa quindi:
dove s è lo spostamento, m è la massa e v la velocità; la formula precedente diventa quindi: 
Il sistema materiale che ho "inventato" è in allegato;
considerando ogni vettore nelle sue componenti x,y,z (
 ) i dati risultano essere:
) i dati risultano essere: 





(dato che prima ho fatto il disegno e poi ho inserito i dati, le masse le ho calcolate in modo che il centro di massa fosse nel punto desisderato)


-----------------------------------------------------------------------------------------------------------------
eseguendo il calcolo secondo la formulazione del 1° teorema di Koenig risulta quindi:



(Il risultato l'ho calcolato a mano facendo i determinanti, con la calcolatrice e con Matlab e torna sempre)
----------------------------------------------------------------------------------------------------------------
Adesso calcolo il momento angolare complessivo senza il teorema di Koenig che deve risultare uguale a quello appena calcolato:
Calcolo prima gli spostamenti e le velocità assolute:




dopodichè eseguo il calcolo:


I 2 risultati non coincidono (c'è una discrepanza di 30 tra i 2 valori ... 366.73 contro 396.73) e non riesco a capire cosa non torni.. ho provato anche a cambiare le procedure di calcolo ma i risultati rimangono sempre questi. Qualcuno saprebbe aiutarmi? Grazie e scusate il papiro
P.s.1 è possibile che il sistema che mi sono inventato infranga le condizioni iniziali per cui le formule che ho scritto sopra sono vere o che alcuni valori per forza correlati non rispettino le leggi che li correlano? Ci ho ragionato molto e mi sembra che sia tutto ok da questo punto di vista
P.s.2 questo è il listato matlab che ho utilizzato per il calcolo (oltre ad aver controllato tutto con la calcolatrice a mano, ottenendo gli stessi risultati)
- Codice: Seleziona tutto
%% VERIFICA 1° TEOREMA DI KOENIG
s_cm = [4;0;0] %poszione centro di massa [m]
sr_1 = [-1;sqrt(3);0] %posiz. rel. del punto 1 rispetto al CM [m]
sr_2 = [0.75;(-3*sqrt(3))/4;0] %posiz. rel. del punto 2 rispetto al CM [m]
m1 =11.25 %[kg]
m2=15 %[kg]
m_tot = m1+m2 %[kg]
v_cm=[0;3;0] %velocità assoluta CM [m/s]
vr_1 = [-1.5;0;0] %v. rel. punto 1 rispetto a CM [m/s]
vr_2 = [sqrt(3)/2;0.5;0] %v. rel. punto 2 rispetto a CM [m/s]
%% Momento angolare totale con 1° teorema di Koenig
%l_tot = l_cm_ass + sum(l_rel_i)
l_tot_koenig = cross(s_cm,m_tot*v_cm)+cross(sr_1,m1*vr_1)+cross(sr_2,m2*vr_2)
%% Momento angolare totale con "momenti assoluti"
%% modo 1 senza t. koenig
s_ass_1 = s_cm+sr_1 %spostamento assoluto del punto 1 [m]
s_ass_2 = s_cm+sr_2 %spostamento assoluto del punto 2 [m]
v_ass_1 = v_cm+vr_1 %velocità assoluta del punto 1 [m/s]
v_ass_2 = v_cm+vr_2 %velocità assoluta del punto 2 [m/s]
%questo conto non torna
l_tot_1 = cross(s_ass_1,m1*v_ass_1)+cross(s_ass_2,m2*v_ass_2)
%% modo 2 senza t. koenig
%Provo a fare singolarmente tutte le coppie di prodotti vettoriali
A=cross(sr_1,m1*vr_1);
B=cross(sr_2,m2*vr_2);
C=cross(s_cm,m1*vr_1);
D=cross(s_cm,m2*vr_2);
E=cross(sr_1,m1*v_cm);
F=cross(sr_2,m2*v_cm);
G=cross(s_cm,m1*v_cm);
H=cross(s_cm,m2*v_cm);
l_tot_2 = A+B+C+D+E+F+G+H %neanche questo conto torna
%% modo 3 senza t. koenig
%Provo a raggruppare diversamente i calcoli
l_ass_1 = m1*(cross(s_cm,v_cm)+cross(s_cm,vr_1)+cross(sr_1,v_cm)+cross(sr_1,vr_1));
l_ass_2 = m2*(cross(s_cm,v_cm)+cross(s_cm,vr_2)+cross(sr_2,v_cm)+cross(sr_2,vr_2));
l_tot_3 = l_ass_1+l_ass_2 %neanche questo conto torna
%se si tolgono le 2 componenti sotto l_tot_3 torna, ma queste componenti
%dovrebbero essere 0 e invece la seconda fa [0 0 30]
%cross(s_cm,m1*vr_1)
%cross(s_cm,m2*vr_2)

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)



 dove v_j è la velocità assoluta del j-esimo punto materiale
dove v_j è la velocità assoluta del j-esimo punto materiale