Elettrotecnica e non solo (admin)
Un gatto tra gli elettroni (IsidoroKZ)
Esperienza e simulazioni (g.schgor)
Moleskine di un idraulico (RenzoDF)
Il Blog di ElectroYou (webmaster)
Idee microcontrollate (TardoFreak)
PICcoli grandi PICMicro (Paolino)
Il blog elettrico di carloc (carloc)
DirtEYblooog (dirtydeeds)
Di tutto... un po' (jordan20)
AK47 (lillo)
Esperienze elettroniche (marco438)
Telecomunicazioni musicali (clavicordo)
Automazione ed Elettronica (gustavo)
Direttive per la sicurezza (ErnestoCappelletti)
EYnfo dall'Alaska (mir)
Apriamo il quadro! (attilio)
H7-25 (asdf)
Passione Elettrica (massimob)
Elettroni a spasso (guidob)
Bloguerra (guerra)
Indice |
Abstract
Tra gli enigmi che assillano gli studenti di elettrotecnica, ci sono i versi delle correnti e le polarità delle tensioni. Spesso, al momento di scrivere le equazioni di Kirchhoff, molti si chiedono come si scelgono i versi o le polarità. Non so quante volte ho ripetuto l'avverbio" arbitrariamente" o l'aggettivo "arbitrario", ma a molti di essi sembrano parole da non considerare, quasi fossero una presa in giro. Sembra non valere l'osservazione che le grandezze incognite, non lo sono solo in valore ma anche in verso che, algebricamente, è il segno del numero che rappresenta il loro valore. Se le grandezze sono note, lo sono sia in valore che in segno ed in quel caso si può fare a meno di scegliere arbitrariamente verso o polarità; ma anche in quel caso, volendolo, si può arbitrariamente scegliere verso o polarità, quindi attribuire immediatamente il segno alla grandezza scelta in base a quella nota. Ma c'è allora chi considera arbitrari i termini noti: insomma una bella lotta e qualche volta mi tocca alzare bandiera bianca
Bipolo
Il bipolo elettrico è un oggetto racchiuso in un determinato volume che è sede di trasformazioni energetiche. E' accessibile per mezzo di due terminali facenti capo ciascuno ad un morsetto. L'energia scambiata con l'esterno nell'unità di tempo è la potenza. La potenza non entra (o esce) dai terminali, ma fluisce attraverso la superficie che delimita il volume. E' il campo elettromagnetico ricavabile dalle grandezze tensione e corrente, che descrivono il comportamento elettrico ai morsetti, che consente lo scambio: campo elettrico e campo magnetico danno origine al vettore di Poynting che indica il flusso della potenza attraverso il volume che delimita il bipolo.
Il segno della potenza
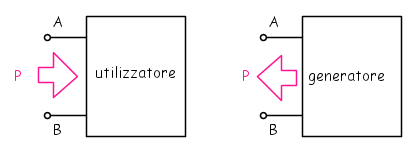
Quando la potenza entra nel bipolo si dice che esso è un utilizzatore; quando ne esce si dice che è un generatore.
Nella figura seguente il bipolo è rappresentato da un rettangolo ed i terminali di accesso con l'esterno sono segmenti i cui estremi, i morsetti, sono indicati con A e B. Il flusso di potenza è indicato con la freccia P che entra nel volume del bipolo nell'utilizzatore, e ne esce nel generatore.
Se non si conosce la natura del bipolo si può ipotizzarne una delle due. Con tale ipotesi si assume arbitrariamente un verso per la potenza. Ad esempio, nella figura che segue, è quello indicato dalle frecce nel caso di assumere, rispettivamente, l'ipotesi di un utilizzatore o di generatore.
Nel caso in cui il flusso di potenza reale coincida con quello arbitrariamente scelto, e che quindi l'ipotesi fatta corrisponda alla realtà energetica del bipolo, il numero che esprime il valore della potenza secondo il verso prefissato, è positivo; negativo in caso contrario.
Riassumendo
| Segno di P | ?=UT | ?=Gen. |
|---|---|---|
| P > 0 | Utilizzatore | Generatore |
| P < 0 | Generatore | Utilizzatore |
Una potenza negativa indica dunque che il bipolo considerato come utilizzatore è in realtà un generatore o, viceversa, che il bipolo considerato come generatore è in realtà un utilizzatore.
Tensione e corrente
Tensione e corrente sono le grandezze che descrivono il comportamento del bipolo elettrico ai morsetti, dalle quali dipendono valore e verso della potenza.
La corrente, o meglio la sua intensità, rappresenta il flusso di cariche positive che, nell'unità di tempo, attraversano una sezione qualsiasi del bipolo, e che quindi, possiamo dire, si spostano da un terminale all'altro dello stesso.
La tensione è l'energia messa in gioco dall'unità di carica nel trasferimento. Tale energia è, in valore assoluto, la differenza tra le energie possedute dalla carica unitaria in corrispondenza dei morsetti, che è il loro potenziale elettrico. Quindi la tensione è anche detta differenza di potenziale. Il potenziale elettrico dipende da un riferimento cui si attribuisce arbitrariamente il valore nullo. La tensione tra i morsetti non dipende dal valore di riferimento.
L'intensità di corrente si misura in ampere (A) mentre la tensione in volt (V).
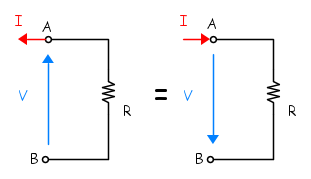
La corrente è rappresentata con un freccia che entra od esce da uno dei due morsetti. Il verso della freccia è arbitrario. Se la corrente reale coincide con quel verso il suo valore in ampere è positivo; in caso contrario è negativo.
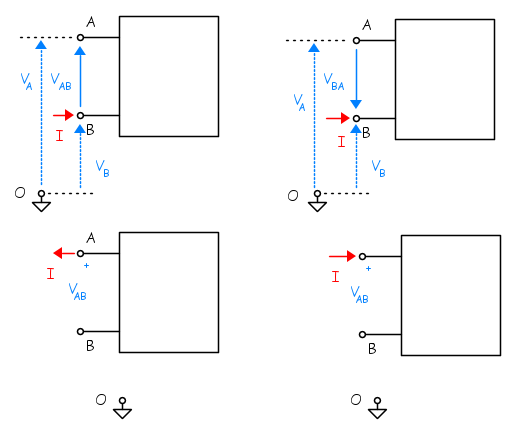
La tensione è pure rappresentata con freccia orientata verso il morsetto che si considera a potenziale più alto, oppure anche da un + posto accanto a quel morsetto.
I morsetti sono contrassegnati con caratteri alfanumerici ed il loro potenziale è indicato con la lettera V che ha come pedice il carattere che lo individua.
La tensione tra un morsetto A ed un morsetto B è indicata con la lettera V (oppure U) che ha come pedici le lettere che individuano i due morsetti; la prima indica il morsetto a potenziale più elevato. Poiché la tensione è, come detto, la differenza dei loro potenziali, si ha, per definizione
VAB = VA − VB
Di conseguenza sarà
VBA = VB − VA = − VAB
- Nota: il potenziale non è altro che la tensione tra il morsetto considerato ed il riferimento adottato. Poiché al riferimento è attribuito il valore zero si ha, ad esempio per il morsetto A: VAO = VA − VO = VA − 0 = VA
La seguente figura illustra quanto detto
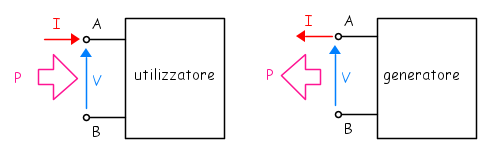
La potenza è il prodotto dell'intensità della corrente per la tensione, P = IV, ed il suo verso coincide con quello della corrente nel morsetto a potenziale più elevato. In ogni bipolo i versi di tensione e corrente possono essere scelti arbitrariamente mentre quello della potenza risulta determinato dalla scelta effettuata. Il disegno che segue rappresenta le due possibilità esistenti che danno luogo, rispettivamente, alla convenzione di utilizzatore e di generatore.
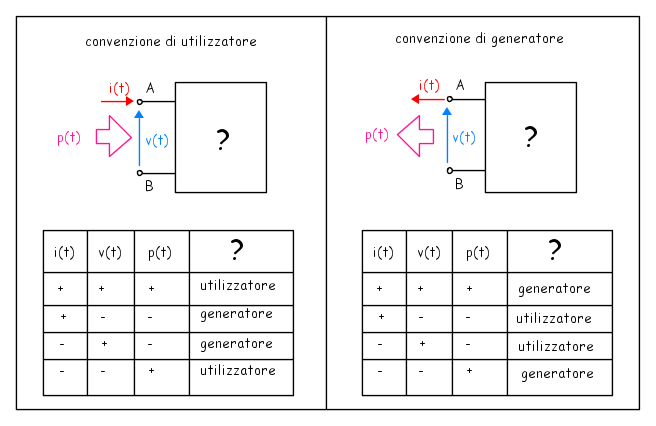
Tensione corrente e potenza sono in generale funzioni del tempo. I loro valori istantanei reali possono essere sia concordi che discordi con quelli prefissati per cui un bipolo può variare nel tempo la sua funzione. Le tabelle nel disegno seguente illustrano tutte le possibilità che si hanno nel caso delle due possibili convenzioni per quanto riguarda la scelta dei versi
Tutte le leggi costitutive dei componenti elettrici nonché le leggi sui circuiti elettrici necessitano della precisazione dei versi assunti per le tensioni e per le correnti che possono essere scelte arbitrariamente.
Legge di Ohm
Sono in pochi a non sapere che la legge di Ohm dice che la tensione è il prodotto "erre per i", ma spesso alcuni dimenticano che affinché l'affermazione sia corretta, occorre stabilire quali sono il verso della corrente e la polarità della tensione da considerare. La possibilità di scelta arbitraria delle stesse porta a quattro possibili configurazioni che, in realtà, si riducono a due, riassumibili con corrente entrante nel terminale a potenziale più alto o corrente uscente da quel terminale, rispettivamente chiamate, come già visto nei precedenti paragrafi, convenzione di utilizzatore e convenzione di generatore
Convenzione di utilizzatore
La legge di Ohm in questo caso si scrive proprio come tutti la conoscono
V = RI
dove R è una quantità positiva. Del resto il resistore può essere solo un utilizzatore e l'energia elettrica che riceve viene integralmente trasformata in calore. La potenza P = VI = RI2 è positiva come deve essere per la convenzione adottata.
Convenzione del generatore
Se si adotta la convenzione del generatore la legge di Ohm dovrà essere scritta in questo modo
V = − RI
La potenza P = VI = − RI2 è un numero negativo, cioè il resistore non genera potenza ma la assorbe o utilizza che dir si voglia.
- Nota: quanto sopra è valido anche quando tensione e corrente sono variabili: cambia il valore della potenza, ma il segno si mantiene sempre lo stesso qualunque sia la convenzione adottata.
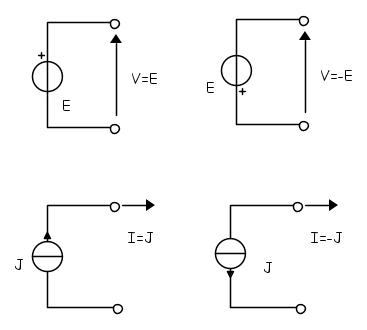
Generatori ideali
Se il bipolo è un generatore ideale noto di tensione o di corrente, nulla vieta (anche se è un po' masochistico) di scegliere ancora arbitrariamente il verso della rispettiva grandezza descrittiva; basta far concordare ciò che è noto con la scelta effettuata, come mostrato nella seguente figura.
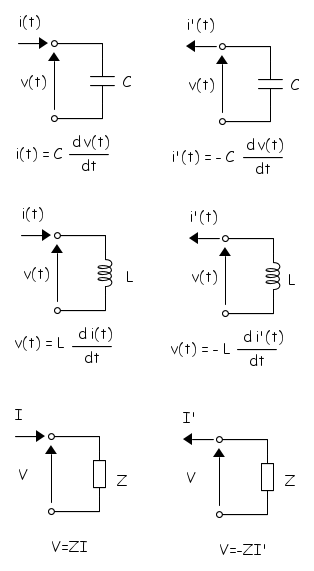
Condensatore, induttore, impedenza
Quanto visto per la legge di Ohm, vale anche per qualsiasi altro bipolo. Nella figura seguente le varie situazioni
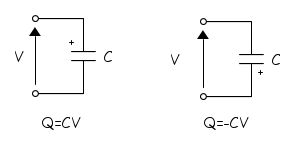
In condizioni statiche la legge costitutiva del condensatore è Q = CV dove Q è la carica del condensatore che coincide con il valore assoluto della carica su una delle due armature. L'armatura con carica positiva è quella collegata al morsetto a potenziale più alto, quindi, fissato il verso della tensione, scrivere la formula con il più significa riferirsi alla carica sull'armatura indicata dalla freccia della tensione. Se indicassimo come positiva l'altra armatura dovremmo cambiare il segno.
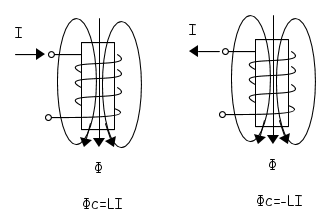
Un discorso simile si può fare per la legge costitutiva dell'induttanza, Φc = LI, dove Φc è il flusso concatenato con il circuito ed I l'intensità di corrente che lo produce. In questo caso il simbolo adottato però non ci dà informazioni sul verso del flusso. Si deve evidenziare l'avvolgimento come nella seguente figura. Si ha il segno positivo quando la corrente e il flusso sono associati secondo la regola del pugno destro chiuso con pollice alzato: le dita chiuse sono il verso della corrente, il pollice indica il verso del flusso che essa produce. Se si inverte il segno della corrente e si mantiene inalterato quello del flusso, occorre il segno meno.
n-polo
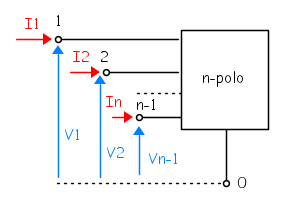
Un n-polo è un oggetto da cui fuoriescono n terminali che terminano in n morsetti. Si può considerare un qualsiasi morsetto come riferimento ed effettuare tutte le considerazioni fatte per il bipolo per ogni coppia di morsetti che comprenda il morsetto di riferimento.
La figura mostra la convenzione generalmente adottata nello scegliere i versi di tensione e corrente che è quella di utilizzatore per ogni bipolo parziale.
Principi di Kirchhoff
I due principi di Kirchhoff, noti anche come legge delle correnti (LKI) e legge delle tensioni (LKV), stabiliscono le relazioni algebriche cui devono soddisfare tensioni e correnti descrittive di bipoli ed n-poli quando sono collegati a formare una rete.
Il collegamento consiste nell'unire morsetti. Due o più morsetti uniti si fondono in un unico morsetto. Quando i morsetti uniti sono almeno tre, il morsetto "fusione" si chiama nodo.
LKI
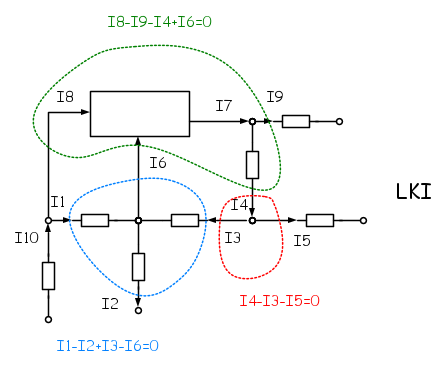
Il primo principio di Kirchhoff, la LKI, afferma che considerata una qualsiasi superficie chiusa che interseca i terminali dei componenti, la somma algebrica delle correnti deve essere nulla. Vanno considerate con un segno, generalmente il più, le correnti con verso entrante nella superficie, con segno contrario quelle uscenti, per cui si può dire anche che la somma aritmetica delle correnti entranti è uguale alla somma aritmetica di quelle uscenti.
- Nota: in genere ci si riferisce ai nodi, e la superficie chiusa è quella che racchiude un nodo, ma il principio è più generale e la superficie chiusa può essere qualsiasi.
Nella figura seguente sono illustrati alcuni esempi. Le superfici chiuse considerate intersecano il piano del disegno secondo le le tratteggiate colorate e le LKI che vi corrispondono sono scritte con il colore della linea.
LKV
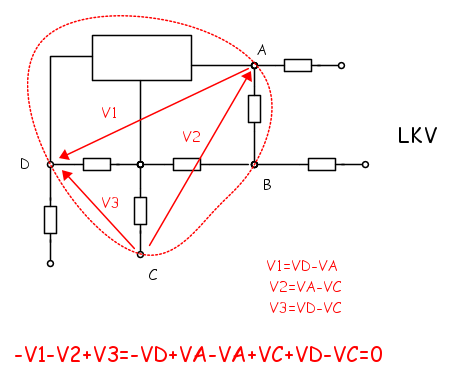
Se si considera una qualsiasi linea chiusa che unisce i morsetti dei componenti che costituiscono una rete, la somma algebrica delle tensioni tra i morsetti è nulla. Indicate le tensioni tra i morsetti in uno dei modi, ad esempio con la freccia orientata arbitrariamente verso il morsetto che si ipotizza a potenziale più alto, e scelto un verso di percorrenza della linea, si considerano con un certo segno, ad esempio positivo, le tensioni che hanno verso concorde, con segno opposto le altre. La figura che segue mostra un esempio giustificando anche il principio in base alla definizione della tensione come differenza di potenziale
In genere il primo principio non genera grandi difficoltà negli studenti; molte di più il secondo e, per quanto si ripeta che il verso delle tensioni, come quello delle correnti, lo sceglie arbitrariamente, la cosa viene dimenticata, o non considerata ed il dubbio prevale, per cui frequenti sono le domande sul forum in cui si chiede: ma come si sceglie il segno della tensione? Riporto qui una delle tante risposte che ho dato.
- Prendi una moneta e la lanci in aria: se viene testa prendi il verso della tensione con un segno, se viene croce con quello opposto.
- Quando hai completato questa operazione per ogni coppia di nodi, lanci ancora in aria la moneta: se viene testa decidi di camminare lungo il percorso chiuso di cui fanno parte le tensioni, in un uno dei due versi possibili (orario, antiorario), se viene croce in quello opposto.
- A questo punto scrivi l'equazione in questo modo: se camminando lungo il verso scelto a caso, hai la tensione parziale, scelta a pure caso, concorde con il verso di percorrenza, le attribuisci il segno che preferisci (positivo o negativo), se è discorde quello opposto. Fai questo fino a quando hai completato il percorso, quindi poni la somma algebrica che ti risulta uguale a zero.
Naturalmente se la tensione di un ramo è nota in valore e polarità, o anche solo come polarità, in quanto ad esempio è indicata, si può fare a meno di lanciare in aria la moneta, ma, volendolo si può ancora fare, imponendo poi alle scelte arbitrarie la condizione imposta da ciò che è noto.
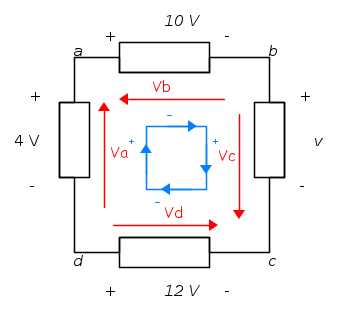
Nel precedente schema le tensioni di tre rami sono note, in valore e segno; della quarta si chiede il valore per una polarità data. Le frecce rosse rappresentano le scelte arbitrarie per le tensioni e, per esse, è scritta la LKV
Va − VB + Vc − Vd = 0
Tali tensioni arbitrarie devono rispettare le condizioni date. Il che implica
Sostituendo nella precedente equazione si ottiene l'equazione che permette di ricavare V e che si sarebbe potuta scrivere immediatamente essendo date le tensioni nei rami.
+ 4 − 10 − V + 12 = 0
Limiti di validità dei principi di Kirchhoff
Non è questa la sede per una discussione di questo genere, molto difficile tra l'altro, che richiede l'analisi delle equazioni di Maxwell per il campo elettromagnetico. Mi limito a ricordare che la loro validità è legata alla frequenza con cui variano le grandezze elettriche; in particolare dipende dalle dimensioni dei circuiti in relazione alla lunghezza d'onda dell'onda elettromagnetica determinata da quella frequenza (condizione di Abraham). Per cercare di capire si può iniziare con il bel post di RenzoDF, per poi approfondire con testi su Teoria dei circuiti.
Legge di Faraday-Lenz
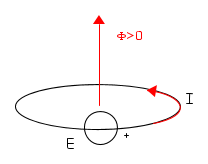
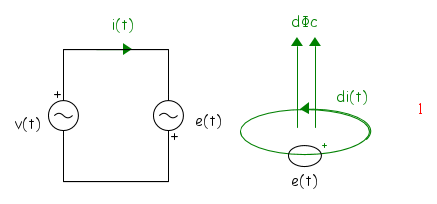
La legge stabilisce un legame tra il flusso magnetico che attraversa le spire di un avvolgimento dando luogo al flusso con esso concatenato e la tensione che si manifesta (indotta) nella spira per effetto della variazione del flusso. Assegnato un verso positivo al flusso, si considera il verso della corrente che, circolando nella, spira dà luogo ad un flusso concorde; tale verso si ricava secondo la regola della vite destrogira. Il polo positivo del generatore che rappresenta la tensione indotta è quello dal quale esce la corrente, come illustrato nel disegno seguente.
La legge, come noto, afferma che la tensione indotta è data dal rapporto tra la variazione del flusso concatenato con l'avvolgimento considerato, ed il tempo in cui tale variazione avviene (più precisamente dalla derivata del flusso concatenato), e che la polarità della tensione è tale da opporsi alla variazione di flusso. La tensione indotta deve aver perciò una polarità tale da far circolare una corrente che dia luogo ad un flusso opposto alla variazione. Per le scelte effettuate circa i versi positivi, facendo riferimento alla seguente figura in cui è indicata la variazione di flusso dΦC ed il verso positivo della tensione che produrrebbe quella variazione
dobbiamo allora scrivere
in quanto la forza elettromotrice indotta deve far circolare una corrente che dia luogo ad un flusso di verso opposto a quello della variazione.
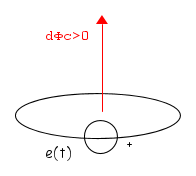
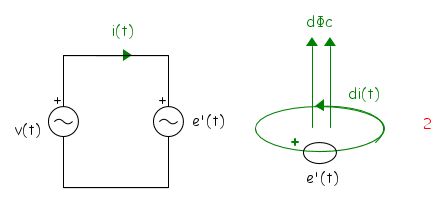
Nulla vieterebbe di considerare positivo il verso opposto per la tensione indotta come mostrato nella seguente figura
In questo caso però dovremo scrivere
Finora non si è specificato chi produce il flusso. Può essere una corrente esterna al circuito che consideriamo, ma può essere la stessa corrente che percorre il circuito. Questo flusso, tra l'altro, c'è sempre, quindi sempre esisterà la tensione indotta da esso, che si dirà di tensione di autoinduzione. Il flusso concatenato per autoinduzione, come tra l'altro abbiamo già scritto più sopra, è esprimibile con il prodotto ΦC = LI dove L è il coefficiente di autoinduzione dipendente dalle caratteristiche fisiche e geometriche del circuito, ed I è la corrente del circuito (in genere un avvolgimento)
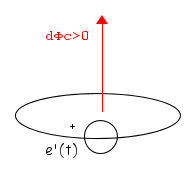
Affinché nel circuito possa circolare una corrente variabile i(t), deve in esso agire una tensione variabile che indicheremo con v(t). La corrente i(t) produrrà dunque un flusso variabile concatenato con il circuito ΦC = Li(t) quindi una tensione indotta. Se manteniamo la convenzione adottata comunemente per la polarità di questa tensione, ci riferiremo al circuito di figura
quindi scriveremo per la LKV
Come detto, nulla vieterebbe di considerare opposto il verso positivo della tensione indotta
nel qual caso dovremmo scrivere
Potremmo sbizzarrirci scegliendo positivo il verso opposto per la corrente, come se cioè, non fosse il generatore v(t) a provocarla
Se indichiamo i versi di v(t) e della tensione indotta come in figura
dovremo scrivere
Mutua induzione
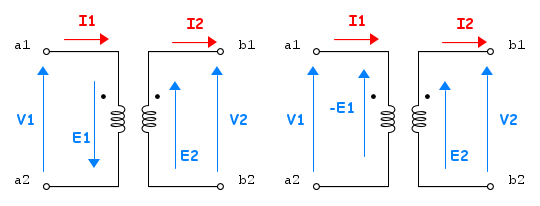
Quando tra due circuiti c'è un accoppiamento magnetico il flusso prodotto da un circuito può aggiungersi o sottrarsi a quello prodotto dall'altro. Nel primo caso il coefficiente di mutua induzione, che definisce l'accoppiamento è positivo; nell'altro negativo. Se il circuito magnetico è noto, quindi è noto anche il senso in cui sono avvolti gli avvolgimenti, il valore di M, compreso il suo segno, è deducibile dai calcoli di risoluzione del circuito magnetico.
Quando gli avvolgimenti sono rappresentati con il simbolo dell'induttanza, l'accoppiamento deve essere specificato sia in valore che in segno. Per stabilire il segno si usa la regola del puntino. Accanto ad un morsetto di ciascuna delle due induttanza accoppiate, viene posto un circoletto nero. Quando le correnti nelle induttanze sono scelte in modo che entrambe entrano o entrambe escono dal morsetto indicato dal circoletto, il coefficiente di mutua induttanza è positivo; in caso contrario è negativo.
L'argomento è stato trattato in un precedente articolo, nel paragrafo il segno di M.
Vale ancora la pena di osservare che se le correnti nei due avvolgimenti sono delle incognite da determinare, il loro verso si sceglie sempre ad arbitrio, ed in base a quel verso si scrive l'equazione con il segno di M determinato dalla precedente regola, come mostrato negli esercizi dell'articolo citato in precedenza.
Trasformatore
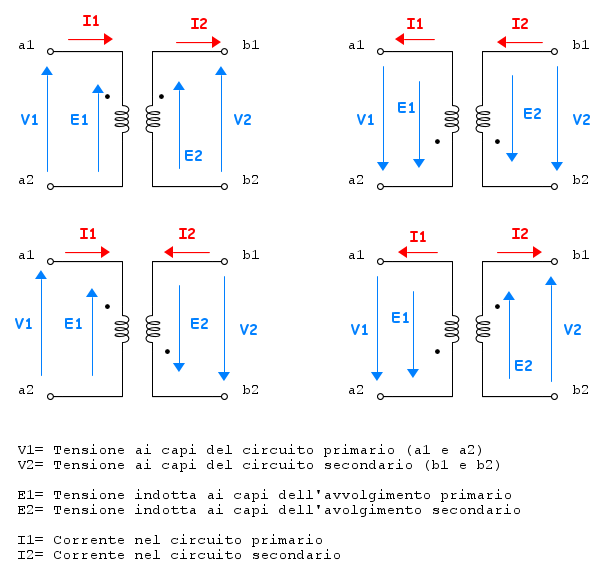
Un trasformatore è, sostanzialmente, una coppia di avvolgimenti magneticamente accoppiati. L'avvolgimento alimentato è il primario, l'altro il secondario cui vanno collegati i bipoli da alimentare. Può essere utile sapere qual è il morsetto positivo del secondario quando si conosce quello del primario. Tale informazione è fornita con il circoletto di cui si è parlato nel precedente paragrafo. Quando dunque il morsetto del primario contrassegnato con il circoletto è positivo e la corrente primaria è entrante in esso, il morsetto positivo del secondario è quello contrassegnato dal circoletto e la corrente, detta naturale, è uscente da quel morsetto. Nel forum uno studente ha chiesto di illustrare tutti i casi possibili, che ho illustrato nel disegno che qui ripropongo.
Un'osservazione è però doverosa per quanto riguarda la 
. Nelle figure precedenti è sempre rappresentata come forza controelettromotrice. In altri invece, e direi proprio nel caso della teoria più classica del trasformatore, la è rappresentata come forza elettromotrice e la forza controelettromotrice è la 
Conclusione
Quello che ho cercato di evidenziare in questo articolo, rivolto fondamentalmente agli studenti che iniziano ad esercitarsi con i circuiti elettrici, è dunque che i segni delle grandezze che compaiono nelle equazioni dipendono dai riferimenti (o versi) che per esse si sono scelti arbitrariamente. Certo, in genere si fa la scelta che si ritiene più conveniente per l'elemento considerato, se questo è possibile, ma basta in fondo solo tenere presente che il segno dei risultati che si ottengono dai calcoli, significa semplicemente grandezza con verso concorde a quello scelto, se il segno è positivo, discorde in caso contrario. Ciò che conta è scrivere correttamente le equazioni in base ai versi scelti. Le relazioni tra i moduli delle grandezze non cambiano, ed i loro segni devono essere sempre tali che la realtà fisica sia rispettata, qualunque sia il riferimento scelto per rappresentarle.
Riferimenti vari
Altri articoli nel sito
- Nel segno della potenza
- Potenza in regime sinusoidale
- Circuiti magneticamente accoppiati
- Convenzione di utilizzatore e generatore
- Ambito di validità dei principi di Kirchhoff
- Flussi di potenza
Post nel forum
Link esterni
Bibliografia
- Fondamenti di elettrotecnica: circuiti - Giuseppe Biorci - Ed UTET 1975
