ElectroYou - la comunità dei professionisti del mondo elettrico

Indice

1 Premessa
2 Linee sane
- 2.1 Schematizzazione
- 2.2 Carichi monofase e carico trifase senza neutro
3 Interruzione del neutro di una derivazione monofase
4 Interruzione del neutro della linea trifase
- 4.1 Esempio

Premessa

Con una certa regolarità arrivano nel forum quesiti sui problemi che si verificano con l'interruzione del neutro.
La spiegazione dei fenomeni è un classico della teoria degli impianti trifase e si trova naturalmente in ogni libro nonché in internet. Anche su questo sito c'è già una mia risposta in proposito, di molti anni fa e questo articolo non è altro che una riedizione di quella risposta con qualche schema, qualche formula ed un esempio numerico.

Quasi tutte le distribuzioni monofase alimentate dall'ente distributore sono derivate da una linea trifase utilizzando il neutro. L'utenza monofase è derivata tra una fase ed il neutro. Il neutro della linea trifase costituisce il filo di ritorno comune per le diverse utenze monofasi distribuite sui tre fili. Il neutro è collegato al centro stella del trasformatore e tra le fasi ed il neutro c'è praticamente sempre la tensione stellata del sistema che è, come noto, la tensione concatenata $U$ (tra fase e fase) del sistema trifase diviso la radice quadrata di tre. Questa è la tensione delle utenze monofasi, $E=\frac{U}{\sqrt{3}}$ .

Linee sane

Schematizzazione

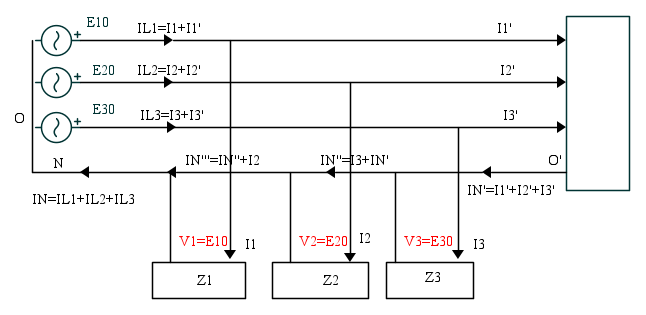
Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Ogni carico trifase con neutro può essere schematizzato con tre carichi monofasi derivati tra ciascuna fase ed il neutro.
Si può quindi considerare solo il seguente schema dove le impedenze sono il parallelo di tutte le impedenze $\dot Z_i$ derivate tra la stessa fase $i$ ed il neutro.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Quando il neutro non è interrotto, la corrente su di esso è la somma vettoriale delle correnti dei carichi sulle tre fasi. Se si trascura l'impedenza delle linee, la tensione sui carichi di ogni fase è la tensione stellata del sistema. Quindi

$\bar I_N= \bar I_{1} + \bar I_{2} + \bar I_{3}$
$\bar V_1=\bar E_{10}$
$\bar V_2=\bar E_{20}$
$\bar V_3=\bar E_{30}$

Carichi monofase e carico trifase senza neutro

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Quando nulla è interrotto, la corrente nel neutro è ancora la somma vettoriale delle correnti dei tre carichi monofasi distribuiti sulle tre fasi. La somma vettoriale delle correnti del carico trifase senza neutro è sempre nulla.

$\bar I_{1}' + \bar I_{2}' + \bar I_{3}' = 0$
Se si trascura l'impedenza delle linee, la tensione sui carichi di ogni fase è la tensione stellata del sistema. Quindi

$\bar I_N= \bar I_{L1} + \bar I_{L2} + \bar I_{L3}= \bar I_{1} + \bar I_{2} + \bar I_{3}$
$\bar V_1=\bar E_{10}$
$\bar V_2=\bar E_{20}$
$\bar V_3=\bar E_{30}$

Interruzione del neutro di una derivazione monofase

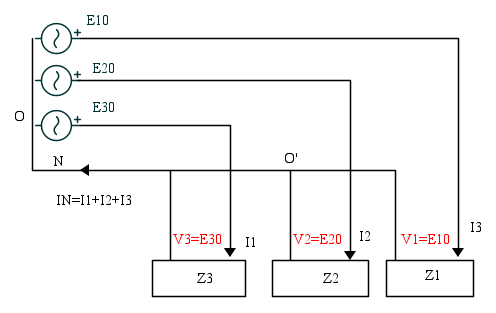
Se si interrompe il neutro della linea che alimenta i carichi su una fase i carichi, la corrente si interrompe e la tensione su di essi si annulla.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Il funzionamento delle altre due fasi non ne risente. Nel caso dello schema, sempre trascurando l'impedenza delle linee si ha

$\bar I_1=0$
$\bar V_1=0$

$\bar V_2=\bar E_{20}$
$\bar V_3= \bar E_{30}$
$\bar I_N=\bar I_1+\bar I_2$

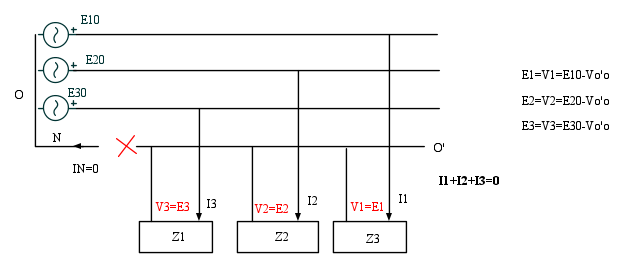
Interruzione del neutro della linea trifase

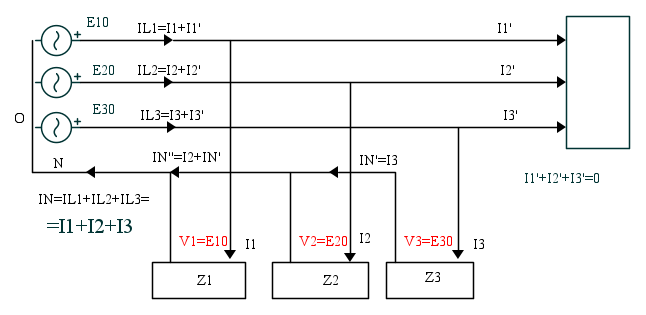
Se si interrompe il neutro della linea trifase, per un guasto, per una manovra errata in cabina, ai carichi monofase manca il filo di ritorno comune che però continuano ad essere alimentati.
L'insieme dei carichi monofase costituisce infatti un carico trifase collegato a stella, con il centro stella collegato ad un neutro che è stato interrotto, quindi isolato. In questa situazione ogni fase costituisce il ritorno delle altre due, ed il potenziale del centro stella assume valori diversi da quello del centro stella del trasformatore di cabina cui, per l'interruzione, non è più collegato. Se nel funzionamento con il neutro il potenziale del centro stella poteva essere identificato con il baricentro del triangolo equilatero costituito dalle tre tensioni concatenate, ora, con il neutro interrotto, potrebbe coincidere ancora con il baricentro solo nel caso che la stella dei carichi monofase fosse equilibrata, cioè nel caso in cui ogni utenza monofase assorbisse la stessa potenza, attiva e reattiva. Solo così le utenze monofasi sarebbero sottoposte ancora alla corretta tensione U=230 V, ma questa è una situazione statisticamente improbabile.
Le utenze monofase formano con molta più probabilità una stella squilibrata, ed il potenziale del loro centrostella si sposta nel piano del triangolo equilatero delle concatenate, tanto più quanto più la stella è squilibrata.
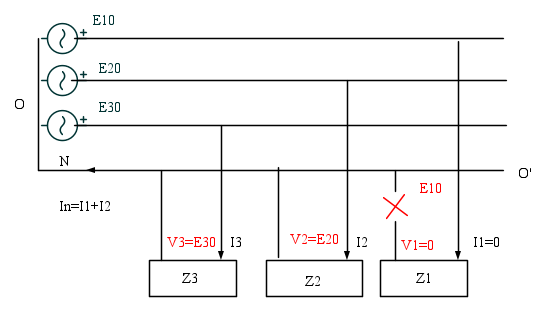
Se una fase è molto più carica delle altre due, cioè assorbe una corrente notevolmente superiore, quindi è caratterizzata da un'impedenza inferiore, il centro stella si sposta verso il vertice del triangolo delle concatenate che corrisponde alla fase maggiormente carica. La tensione in questa utenza monofase si abbassa notevolmente mentre la tensione nelle altre due si innalza. La fase carica sarà dunque sottoposta ad una tensione notevolmente inferiore a 230 V, le altre due ad una tensione sensibilmente superiore. Se supponiamo per semplicità i carichi resistivi, se la resistenza della fase carica diventa trascurabile rispetto a quella delle altre due fasi, in queste ultime la tensione tende al valore della concatenata; quindi 400 invece di 230.
Illustriamo con uno schema ed un grafico vettoriale quanto scritto sopra. Con $\bar E_{i0}$ sono indicate le tensioni stellate ideali del sistema, quelle cioè riferite al baricentro del triangolo delle concatenate, O, mentre con $\bar E_i$ ( che sono le $V i$ )sono indicate le tensioni stellate rispetto al centro stella reale dei carichi, O'.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

In questo caso si ha una tensione tra il centro stella dei generatori $O$ ed il centro stella dei carichi $O'$
Le tensioni sulle derivazioni monofase variano, anche notevolmente rispetto al valore della stellata del sistema.
Applicando Millman si ha

${\bar V_{O'O}} = \frac{{\frac{{{{\bar E}_{10}}}}{{{{\dot Z}_1}}} + \frac{{{{\bar E}_{20}}}}{{{{\dot Z}_2}}} + \frac{{{{\bar E}_{30}}}}{{{{\dot Z}_3}}}}}{{\frac{1}{{{{\dot Z}_1}}} + \frac{1}{{{{\dot Z}_2}}} + \frac{1}{{{{\dot Z}_3}}}}}$
Per tutti i carichi a valle dell'interruzione si ha
$\begin{array}{l}{{\bar V}_1} = {{\bar E}_{10}} - {V_{O'O}}\\{{\bar V}_2} = {{\bar E}_{20}} - {V_{O'O}}\\{{\bar V}_3} = {{\bar E}_{30}} - {V_{O'O}}\\\\{{\bar I}_1} = \frac{{{{\bar V}_1}}}{{{{\dot Z}_1}}}\\{{\bar I}_2} = \frac{{{{\bar V}_2}}}{{{{\dot Z}_2}}}\\{{\bar I}_3} = \frac{{{{\bar V}_3}}}{{{{\dot Z}_3}}}\end{array}$

${\bar I_1} + {\bar I_2} + {\bar I_3} = 0$

Esempio

$\begin{array}{l} {P_1} = 120{\rm{kW;}}\cos {\varphi _1} = 0,95\\ {P_2} = 60{\rm{kW;}}\cos {\varphi _2} = 0,9\\ {P_3} = 30{\rm{kW;}}\cos {\varphi _3} = 0,92 \end{array}$

$\begin{array}{l} {I_1} = \frac{{{P_1}}}{{{E_1}\cos {\varphi _1}}} = \frac{{120000}}{{230 \times 0,95}} = 549{\rm{A}}\\ {Z_1} = \frac{{{E_1}}}{{{I_1}}} = 0,419\Omega \\ {{\dot Z}_1} = 0,419\angle 18,2\Omega \end{array}$

$\begin{array}{l} {I_2} = \frac{{{P_2}}}{{{E_2}\cos {\varphi _2}}} = \frac{{60000}}{{230 \times 0,9}} = 289{\rm{A}}\\ {Z_2} = \frac{{{E_2}}}{{{I_2}}} = 0,796\Omega \\ {{\dot Z}_2} = 0,796\angle 25,8\Omega \end{array}$

$\begin{array}{l} {I_3} = \frac{{{P_3}}}{{{E_3}\cos {\varphi _3}}} = \frac{{30000}}{{230 \times 0,92}} = 142{\rm{A}}\\ {Z_2} = \frac{{{E_2}}}{{{I_2}}} = 1,62\Omega \\ {{\dot Z}_2} = 1,62\angle 23\Omega \end{array}$

$U=400 \, \text{V} \to E_{i0}=231 \, \text{V}$

${U_{O'O}} = 77,5\angle 75 \, {\rm{V}}$

$\bar E_1=\bar V_1=157 \angle 97,3 \, \rm{V}$

$\bar E_2=\bar V_2=261\angle -46.6 \, \rm{V}$

$\bar E_3=\bar V_3=290 \angle -139 \, \rm{V}$

Nella fase più carica la tensione si abbassa, mentre si innalza nelle fasi meno cariche. Se lo squilibrio è consistente, le variazioni di tensione sulle fasi, conseguenti all'interruzione del neutro di linea, superano i valori di tolleranza delle apparecchiature, danneggiandole.

ElectroYou - la comunità dei professionisti del mondo elettrico

Interruzione del neutro

Indice

Premessa

Linee sane

Schematizzazione

Carichi monofase e carico trifase senza neutro

Interruzione del neutro di una derivazione monofase

Interruzione del neutro della linea trifase

Esempio

Inserisci un commento

Informazioni

Seguici

Pubblicità

Credits